练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．甲、乙两人参加某商场的招聘测试，测试由语言和商品知识两个项目组成，他们各自的成绩（百分制）如下表所示．该商场根据成绩在两人之间录用了乙，则本次招聘测试中权重较大的是语言项目．
    应聘者语言商品知识
    甲7080
    乙8070

    分析 设语言类的权重为x（0＜x＜1），则商品知识的权重为（1-x），根据甲的平均成绩小于乙的平均成绩列出不等式，求解可得．

    解答 解：设语言类的权重为x（0＜x＜1），则商品知识的权重为（1-x），
    根据题意得：70x+80（1-x）＜80x+70（1-x），
    解得：x＞0.5，
    ∴本次招聘测试中权重较大的是语言项目，
    故答案为：语言．

    点评 本题主要考查加权平均数的计算，熟练掌握加权平均数的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列说法正确的是（　　）
    A．没有加减运算的代数式是单项式B．单项式$\frac{3{x}^{2}y}{4}$的系数是3，次数是2
    C．单项式x既没有系数，也没有次数D．单项式-a2bc的系数是-1，次数是4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

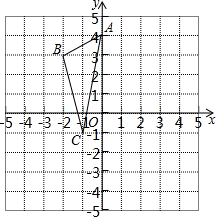    1．如图，网格中每个小正方形的边长均为1，已知三角形ABC及三角形外一点D，平移三角形ABC使点A（0，4）移动到点D（3，2），得到三角形DEF，B（-2，3）的对应点为E，C（-1，-1）对应点F．
    （1）画出三角形DEF；
    （2）写出点E、F的坐标；
    （3）直接写出三角形ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

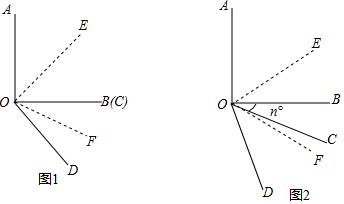
    18．如图，若∠DAE=∠E，∠B=∠D，那么AB∥DC吗？请在下面的解答过程中填空或在括号内填写理由．
    解：理由如下：
    ∵∠DAE=∠E，（已知）
    ∴AD∥BE，（内错角相等，两直线平行）
    ∴∠D=∠DCE．（两直线平行，内错角相等）
    又∵∠B=∠D，（已知）
    ∴∠B=∠DCE．（ 等量代换）
    ∴AB∥DC，（同位角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．通过配方，确定抛物线y=ax2+bx+1的顶点坐标及对称轴，其中a=sin30°-tan45°，b=4tan30°•sin60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．因式分解：16a3-16a2+4a=4a（2a-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．2013年，某市一楼盘以毎平方米5000元的均价对外销售．因为楼盘滞销，房地产开发商为了加快资金的周转，决定进行降价促销，经过连续两年的下调后，2015年的均价为每平方米4050元．
    （1）求平均每年下调的百分率；
    （2）假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金45万元，张强的愿望能否实现？（房价每平方米按照均价计算）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知∠AOB=90°，∠COD=30°，OE平分∠AOC，OF平分∠BOD．
    （1）如图1，当OB、OC重合时，求∠EOF的度数．
    （2）当∠COD从图1所示位置绕点O顺时针旋转n°（0＜＜90）时，如图2，∠AOE-∠BOF的值是否为定值？若是定值，求出∠AOE-∠BOF的值，若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知：关于x的方程x2-（m+2）x+m+1=0．
    （1）求证：该方程总有实数根；
    （2）若二次函数y=x2-（m+2）x+m+1（m＞0）与x轴交点为A，B（点A在点B的左边），且两交点间的距离是2，求二次函数的表达式；
    （3）横、纵坐标都是整数的点叫做整点．
    在（2）的条件下，垂直于y轴的直线y=n与抛物线交于点E，F．若抛物线在点E，F之间的部分与线段EF所围成的区域内（包括边界）恰有7个整点，结合函数的图象，直接写出n的取值范围．

    查看答案和解析>>

    同步练习册答案