
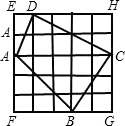
如图,小方格都是边长为1的正方形,则四边形ABCD的面积是( )
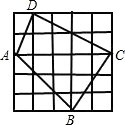
A.25 B.12.5 C.9 D.8.5
B【考点】三角形的面积.
【专题】网格型.
【分析】根据求差法,让大正方形面积减去周围四个直角三角形的面积即可解答.
【解答】解:如图:小方格都是边长为1的正方形,
∴四边形EFGH是正方形,S□EFGH=EF•FG=5×5=25
S△AED=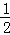 DE•AE=
DE•AE=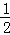 ×1×2=1,
×1×2=1,
S△DCH=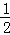 •CH•DH=
•CH•DH=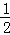 ×2×4=4,
×2×4=4,
S△BCG=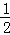 BG•GC=
BG•GC=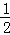 ×2×3=3,
×2×3=3,
S△AFB=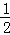 FB•AF=
FB•AF=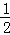 ×3×3=4.5.
×3×3=4.5.
S四边形ABCD=S□EFGH﹣S△AED﹣S△DCH﹣S△BCG﹣S△AFB=25﹣1﹣4﹣3﹣4.5=12.5.
故选:B.
【点评】本题考查的是勾股定理的运用,根据图形可以求出此大正方形的面积和三角形的面积,再用大正方形的面积减去小正方形的面积即可,此题的解法很多,需同学们仔细解答.


科目:初中数学 来源: 题型:
如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,己知AB=AC=5,BC=6,且将△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当点E运动到什么位置时,线段AM最短?并求出此时AM的值.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
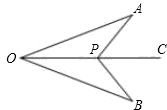
如图,点P是∠AOB的角平分线OC上一点,分别连接 AP、BP,若再添加一个条件即可判定△APO≌△BPO,则在以下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC;④AP=BP;⑤OA=OB,不一定正确的是__________.
(只需填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.

(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com