
如图,在△ABC中,己知AB=AC=5,BC=6,且将△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当点E运动到什么位置时,线段AM最短?并求出此时AM的值.(直接写出答案)

【考点】相似形综合题.
【分析】(1)由AB=AC,根据等边对等角,可得∠B=∠C,又由△ABC≌△DEF与三角形外角的性质,易证得∠CEM=∠BAE,则可证得:△ABE∽△ECM;
(2)首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案;
(3)先设BE=x,由△ABE∽△ECM,根据相似三角形的对应边成比例,易得CM=﹣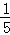 (x﹣3)2+
(x﹣3)2+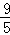 ,利用二次函数的性质,继而求得线段AM的最小值.
,利用二次函数的性质,继而求得线段AM的最小值.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵△ABC≌△DEF,
∴∠AEF=∠B,
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,
∴∠CEM=∠BAE,
∴△ABE∽△ECM;
(2)解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,则△ABE≌△ECM,
∴CE=AB=5,
∴BE=BC﹣EC=6﹣5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴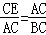 ,
,
∴CE=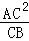 =
=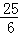 ,
,
∴BE=6﹣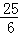 =
=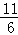 ;
;
∴BE=1或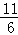 ;
;
(3)解:设BE=x,
又∵△ABE∽△ECM,
∴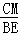 =
= ,
,
即: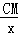 =
= ,
,
∴CM=﹣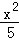 +
+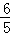 x=﹣
x=﹣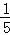 (x﹣3)2+
(x﹣3)2+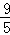 ,
,
∴AM=﹣5﹣CM=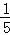 (x﹣3)2+
(x﹣3)2+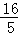 ,
,
∴当x=3时,AM最短为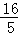 ,
,
∴BE=3时,AM最短为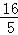 .
.
【点评】此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及二次函数的最值问题.此题难度较大,注意数形结合思想、分类讨论思想与函数思想的应用是解此题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
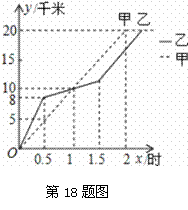
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有个数的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
李大爷一年前买入了A、B两种兔子共46只,目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子 只,目前A、B两种兔子共 只(均用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只,如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
查看答案和解析>>
科目:初中数学 来源: 题型:
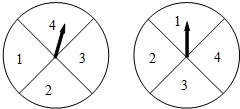
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率等于__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com