练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

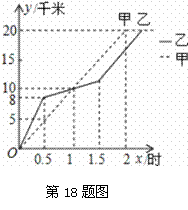
    在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度；②出发后1小时，两人行程均为10km；③出发后1.5小时，甲的行程比乙多3km；④甲比乙先到达终点．其中正确的有个数的序号是           .


    ②③④；


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，透明的圆柱形容器（容器厚度忽略 不计）的高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是…………………（　　）

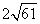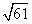    A．13㎝；   B．㎝；   C．㎝； D．㎝；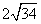

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，∠AOB=30°，点A坐标为（2，0）．过A作⊥OB，垂足为；过作⊥x轴，垂足为；再过点作⊥OB，垂足为点；再过点作⊥x轴，垂足为…；这样一直作下去，则的纵坐标为            ．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某种鲸的体重约为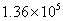㎏，关于这个近似数，下列说法正确的是……………（    ）

    A．它精确到百位；   B．它精确到0.01；C．它精确到千分位；    D．它精确到千位；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在四边形ABCD中，AB∥CD，连接BD．请添加一个适当的条件         ，使△ABD≌△CDB．（只需写一个）

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在正方形ABCD中，G是BC上任意一点，连接AG，DE⊥AG于E，BF∥DE交AG于F，探究线段AF、BF、EF三者之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知：AB=AC，直线m经过点A，点D、E是直线m上两个动点，连接BD、CE．

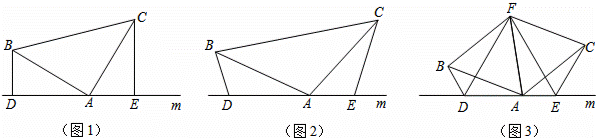
    （1）如图1，若∠BAC=90°，BD⊥DE，CE⊥DE．求证：DE=BD+CE．

    （2）如图2，若∠BAC=∠BDA=∠AEC，则（1）中的结论DE=BD+CE还成立吗？（只回答答案，不用证明）

    （3）如图3，在（2）的条件下，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，是判定△DEF的形状，并证明你的判定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知ab＝4，若－2≤b≤－1，则a的取值范围是    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，己知AB=AC=5，BC=6，且将△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．

    （1）求证：△ABE∽△ECM；

    （2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；

    （3）当点E运动到什么位置时，线段AM最短？并求出此时AM的值．（直接写出答案）

    查看答案和解析>>

    同步练习册答案