
如图,已知:AB=AC,直线m经过点A,点D、E是直线m上两个动点,连接BD、CE.
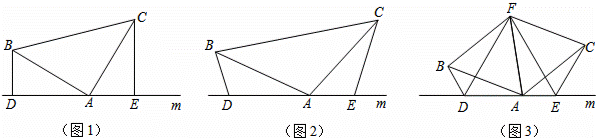
(1)如图1,若∠BAC=90°,BD⊥DE,CE⊥DE.求证:DE=BD+CE.
(2)如图2,若∠BAC=∠BDA=∠AEC,则(1)中的结论DE=BD+CE还成立吗?(只回答答案,不用证明)
(3)如图3,在(2)的条件下,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,是判定△DEF的形状,并证明你的判定.
解:(1)∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵BD⊥AD,∴∠BDA=90°,
∴∠BAD+∠ABD=90°,∴∠DBA=∠CAE; ∵CE⊥DE,∴∠CEA=90°,
∴∠ADB=∠CEA.
在△ADB和△CEA中,
 ,∴△ADB≌△CEA(AAS)∴AD=CE,BD=AE.
,∴△ADB≌△CEA(AAS)∴AD=CE,BD=AE.
∵DE=DA+AE,∴DE=BD+CE;
(2)(1)中的结论DE=BD+CE仍然成立.
理由:∵∠DAB+BAC+∠CAE=180°,∠CAE+∠ACE+∠AEC=180°,
∴∠DAB+∠BAC+∠CAE=∠CAE+∠ACE+∠AEC.∵∠BAC=∠AEC,∴∠DAB=∠ACE.
在△ADB和△CEA中
 ,∴△ADB≌△CEA(AAS)∴AD=CE,BD=AE.∵DE=DA+AE,
,∴△ADB≌△CEA(AAS)∴AD=CE,BD=AE.∵DE=DA+AE,
∴DE=BD+CE;

(3)△DFE是等边三角形.
理由:∵△ADB≌△CEA,∴∠DBA=∠EAC,BD=EA.∵△ABF和△ACF均为等边三角形,∴BF=AB=AF=AC=CF,∠ABF=∠CAF=60°,∴∠ABF+∠DBA=∠CAF+∠EAC,
∴∠DBF=∠EAF.
在△FDB和△FEA中,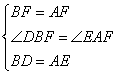 ,∴△FDB≌△FEA(SAS),∴DF=EF,∠DFB=∠EFA.∵∠DFB+∠DFA=60°,∴∠EFA+∠DFA=60°,即∠DFE=60°
,∴△FDB≌△FEA(SAS),∴DF=EF,∠DFB=∠EFA.∵∠DFB+∠DFA=60°,∴∠EFA+∠DFA=60°,即∠DFE=60°
∴△DFE是等边三角形.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
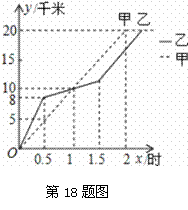
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有个数的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
李大爷一年前买入了A、B两种兔子共46只,目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子 只,目前A、B两种兔子共 只(均用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只,如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com