
如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.

(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)①由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
②由①得到AD=CE,CD=BE,即可求出答案;
(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,代入已知即可得到答案.
【解答】(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
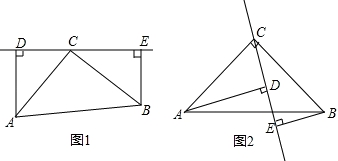
在△ADC和△CEB中,
 ,
,
∴△ADC≌△CEB(AAS).
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
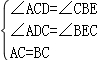 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
【点评】本题主要考查了邻补角的意义,全等三角形的性质和 判定等知识点,能根据已知证出符合全等的条件是解此题的关键,题型较好,综合性比较强.
判定等知识点,能根据已知证出符合全等的条件是解此题的关键,题型较好,综合性比较强.


科目:初中数学 来源: 题型:
已知正比例函数y=k1x的图象与一次函数y=k2x﹣9的图象交于点P(3,﹣6).
(1)求k1,k2的值;
(2)如果一次函数y=k2x﹣9与x轴交于点A,求A点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
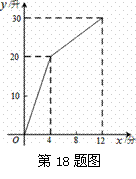
如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起 分钟该容器内的水恰好放完.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com