
ΓΨΧβΡΩΓΩ–ΓΟςΦ“2002ΡξΥΡΗωΦΨΕ»ΒΡ”ΟΒγΝΩ»γœ¬ΘΚ
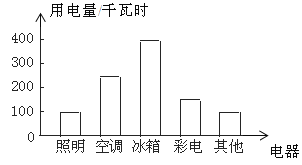
ΦΨΕ»Οϊ≥Τ | ”ΟΒγΝΩΘ®ΒΞΈΜΘΚ«ßΆΏ ±Θ© |
ΒΎ“ΜΦΨΕ» | 250 |
ΒΎΕΰΦΨΕ» | 150 |
ΒΎ»ΐΦΨΕ» | 400 |
ΒΎΥΡΦΨΕ» | 200 |
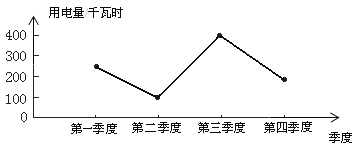
Τδ÷–Ης÷÷ΒγΤς”ΟΒγΝΩ»γœ¬±μΘΚ
Ης÷÷ΒγΤς | ”ΟΒγΝΩΘ®ΒΞΈΜΘΚ«ßΆΏ ±Θ© |
Ω’Βς | 250 |
±υœδ | 400 |
’’Ος | 100 |
≤ Βγ | 150 |
ΤδΥϊ | 100 |
–ΓΟςΗυΨί…œΟφΒΡ ΐΨί÷Τ≥…œ¬ΟφΒΡΆ≥ΦΤΆΦ.
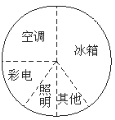
ΗυΨί“‘…œ»ΐΖυΆ≥ΦΤΆΦΜΊ¥πΘΚ
Θ®1Θ©¥”ΡΡΖυΆ≥ΦΤΆΦ÷–Ω…“‘Ω¥≥ωΗςΗωΦΨΕ»”ΟΒγΝΩ±δΜ·«ιΩωΘΩ
Θ®2Θ©¥”ΡΡΖυΆ≥ΦΤΆΦ÷–Ω…“‘Ω¥≥ω±υœδ”ΟΒγΝΩ≥§ΙΐΉή”ΟΒγΝΩΒΡ![]() ΘΩ
ΘΩ
Θ®3Θ©¥”ΡΡΖυΆ≥ΦΤΆΦ÷–Ω…“‘«ε≥ΰΒΊΩ¥≥ωΩ’ΒςΒΡ”ΟΒγΝΩΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©’έœΏΆ≥ΦΤΆΦΘΜΘ®2Θ©…»–ΈΆ≥ΦΤΆΦΘΜΘ®3Θ©Χθ–ΈΆ≥ΦΤΆΦ
ΓΨΫβΈωΓΩ
Θ®1Θ©’έœΏΆ≥ΦΤΆΦ±μ ΨΒΡ « ¬ΈοΒΡ±δΜ·«ιΩωΘΜ
Θ®2Θ©…»–ΈΆ≥ΦΤΆΦ÷±Ϋ”Ζ¥”≥≤ΩΖ÷’ΦΉήΧεΒΡΑΌΖ÷±»¥σ–ΓΘΜ
Θ®3Θ©Χθ–ΈΆ≥ΦΤΆΦΡή«ε≥ΰΒΊ±μ Ψ≥ωΟΩΗωœνΡΩΒΡ ΐΨίΘ°
Θ®1Θ©¥”’έœΏΆ≥ΦΤΆΦΩ…“‘Ω¥≥ωΗςΗωΦΨΕ»”ΟΒγΝΩ±δΜ·«ιΩωΘΜ
Θ®2Θ©±υœδ”ΟΒγΝΩ≥§ΙΐΉή”ΟΒγΝΩΒΡ![]() Θ§ΨΆ «“Σ÷ΣΒά≤ΩΖ÷’ΦΉήΧεΒΡΑΌΖ÷±»¥σ–ΓΘ§Ω…“‘¥”…»–ΈΆ≥ΦΤΆΦΩ…“‘Ω¥≥ωΘΜ
Θ§ΨΆ «“Σ÷ΣΒά≤ΩΖ÷’ΦΉήΧεΒΡΑΌΖ÷±»¥σ–ΓΘ§Ω…“‘¥”…»–ΈΆ≥ΦΤΆΦΩ…“‘Ω¥≥ωΘΜ
Θ®3Θ©Ω’ΒςΒΡ”ΟΒγΝΩΨΆ «“Σ÷ΣΒάœνΡΩΒΡ ΐΨίΘ§Ω…“‘¥”Χθ–ΈΆ≥ΦΤΆΦΩ…“‘Ω¥≥ωΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ,ΨΊ–Έ![]() ÷–,
÷–,![]() ,
,![]() ,
,![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏ
ΒΡ¥Ι÷±ΤΫΖ÷œΏ![]() Ζ÷±πΫΜ
Ζ÷±πΫΜ![]() ΓΔ
ΓΔ![]() ”ΎΒψ
”ΎΒψ![]() ΓΔ
ΓΔ![]() ,¥ΙΉψΈΣ
,¥ΙΉψΈΣ![]() .
.
(1)»γΆΦ,Ν§Ϋ”![]() ΓΔ
ΓΔ![]() .«σ÷ΛΥΡ±Ώ–Έ
.«σ÷ΛΥΡ±Ώ–Έ![]() ΈΣΝβ–Έ,≤Δ«σ
ΈΣΝβ–Έ,≤Δ«σ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
(2)»γΆΦ,Ε·Βψ![]() ΓΔ
ΓΔ![]() Ζ÷±π¥”
Ζ÷±π¥”![]() ΓΔ
ΓΔ![]() ΝΫΒψΆ§ ±≥ωΖΔ,―Ί
ΝΫΒψΆ§ ±≥ωΖΔ,―Ί![]() ΚΆ
ΚΆ![]() Ης±Ώ‘»ΥΌ‘ΥΕ·“Μ÷ή.Φ¥Βψ
Ης±Ώ‘»ΥΌ‘ΥΕ·“Μ÷ή.Φ¥Βψ![]() Ή‘
Ή‘![]() Γζ
Γζ![]() Γζ
Γζ![]() Γζ
Γζ![]() ΆΘ÷Ι,Βψ
ΆΘ÷Ι,Βψ![]() Ή‘
Ή‘![]() Γζ
Γζ![]() Γζ
Γζ![]() Γζ
Γζ![]() ΆΘ÷Ι.‘Ύ‘ΥΕ·Ιΐ≥Χ÷–,
ΆΘ÷Ι.‘Ύ‘ΥΕ·Ιΐ≥Χ÷–,
ΔΌ“―÷ΣΒψ![]() ΒΡΥΌΕ»ΈΣΟΩΟκ5
ΒΡΥΌΕ»ΈΣΟΩΟκ5![]() ,Βψ
,Βψ![]() ΒΡΥΌΕ»ΈΣΟΩΟκ4
ΒΡΥΌΕ»ΈΣΟΩΟκ4![]() ,‘ΥΕ· ±ΦδΈΣ
,‘ΥΕ· ±ΦδΈΣ![]() Οκ,Β±
Οκ,Β±![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–Έ ±,«σ
ΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–Έ ±,«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
ΔΎ»τΒψ![]() ΓΔ
ΓΔ![]() ΒΡ‘ΥΕ·¬Ζ≥ΧΖ÷±πΈΣ
ΒΡ‘ΥΕ·¬Ζ≥ΧΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() (ΒΞΈΜ:
(ΒΞΈΜ:![]() ,
,![]() ),“―÷Σ
),“―÷Σ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–Έ,–¥≥ω
ΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–Έ,–¥≥ω![]() ”κ
”κ![]() ¬ζΉψΒΡ ΐΝΩΙΊœΒ Ϋ.(÷±Ϋ”–¥≥ω¥πΑΗΘ§≤Μ“Σ«σ÷ΛΟς)
¬ζΉψΒΡ ΐΝΩΙΊœΒ Ϋ.(÷±Ϋ”–¥≥ω¥πΑΗΘ§≤Μ“Σ«σ÷ΛΟς)

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΦΪ¥σΒΊ¬ζΉψ»ΥΟώ…ζΜνΒΡ–η«σΘ§ΖαΗΜ –≥ΓΙ©”ΠΘ§Ρ≥«χ≈©¥εΈ¬≈ο…η ©≈©“Β―ΗΥΌΖΔ’ΙΘ§Έ¬≈ο÷÷÷≤ΟφΜΐ‘Ύ≤ΜΕœά©¥σΘ°‘ΎΗϊΒΊ…œ≈ύ≥…“Μ––“Μ––ΒΡ≥ΛΖΫ–ΈΆΝΙΓΘ§Α¥Υ≥–ρΦδΗτ÷÷÷≤≤ΜΆ§≈©ΉςΈοΒΡΖΫΖ®Ϋ–Ζ÷¬ΔΦδΗτΧΉ÷÷Θ°ΩΤ―ß―–ΨΩ±μΟςΘΚ‘ΎΥήΝœΈ¬≈ο÷–Ζ÷¬ΔΦδΗτΧΉ÷÷ΗΏΓΔΑΪ≤ΜΆ§ΒΡ Ώ≤ΥΚΆΥ°Ιϊ(Ά§“Μ÷÷ΫτΑΛ‘Ύ“ΜΤπ÷÷÷≤≤Μ≥§ΙΐΝΫ¬Δ)Θ§Ω…‘ωΦ”ΥϋΟ«ΒΡΙβΚœΉς”ΟΘ§ΧαΗΏΒΞΈΜΟφΜΐΒΡ≤ζΝΩΚΆΨ≠ΦΟ–ß“φΘ°
œ÷”–“ΜΗω÷÷÷≤ΉήΟφΜΐΈΣ540 m2ΒΡ≥ΛΖΫ–ΈΥήΝœΈ¬≈οΘ§Ζ÷¬ΔΦδΗτΧΉ÷÷≤ίί°ΚΆΈςΚλ ΝΙ≤24¬ΔΘ§÷÷÷≤ΒΡ≤ίί°ΜρΈςΚλ ΝΒΞ÷÷≈©ΉςΈοΒΡΉή¬Δ ΐ≤ΜΒΆ”Ύ10¬ΔΘ§”÷≤Μ≥§Ιΐ14¬Δ(¬Δ ΐΈΣ’ΐ’ϊ ΐ)Θ§ΥϋΟ«ΒΡ’ΦΒΊΟφΜΐΓΔ≤ζΝΩΓΔάϊ»σΖ÷±π»γœ¬ΘΚ
’ΦΒΊΟφΜΐ(m2/¬Δ) | ≤ζΝΩ(«ßΩΥ/¬Δ) | άϊ»σ(‘Σ/«ßΩΥ) | |
ΈςΚλ Ν | 30 | 160 | 1.1 |
≤ίί° | 15 | 50 | 1.6 |
(1)»τ…η≤ίί°Ι≤÷÷÷≤ΝΥ![]() ¬ΔΘ§Ά®ΙΐΦΤΥψΥΒΟςΙ≤”–ΦΗ÷÷÷÷÷≤ΖΫΑΗΘ§Ζ÷±π «ΡΡΦΗ÷÷ΘΜ
¬ΔΘ§Ά®ΙΐΦΤΥψΥΒΟςΙ≤”–ΦΗ÷÷÷÷÷≤ΖΫΑΗΘ§Ζ÷±π «ΡΡΦΗ÷÷ΘΜ
(2)‘Ύ’βΦΗ÷÷÷÷÷≤ΖΫΑΗ÷–Θ§ΡΡ÷÷ΖΫΑΗΜώΒΟΒΡάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΩΣΖΔ…ΧΫχ––…ΧΤΧ¥ΌœζΘ§ΙψΗφ…œ–¥Ή≈»γœ¬ΧθΩνΘΚΆΕΉ ’ΏΙΚ¬ρ…ΧΤΧΚσΘ§±Ί–κ”…ΩΣΖΔ…Χ¥ζΉβΝό5ΡξΘ§5ΡξΤΎ¬ζΚσ”…ΩΣΖΔ…Χ“‘±»‘≠…ΧΤΧ±ξΦέΗΏ20%ΒΡΦέΗώΫχ––ΜΊΙΚΘ§ΆΕΉ ’ΏΩ…‘Ύ“‘œ¬ΝΫ÷÷ΙΚΤΧΖΫΑΗ÷–Ήω≥ω―Γ‘ώΘΚ
ΖΫΑΗ“ΜΘΚΑ¥’’…ΧΤΧ±ξΦέ“Μ¥Έ–‘ΗΕ«εΤΧΩνΘ§ΟΩΡξΩ…ΜώΒΟΒΡΉβΫπΈΣ…ΧΤΧ±ξΦέΒΡ10%ΘΜ
ΖΫΑΗΕΰΘΚΑ¥…ΧΤΧ±ξΦέΒΡΑΥ’έ“Μ¥Έ–‘ΗΕ«εΤΧΩνΘ§«Α3Ρξ…ΧΤΧΒΡΉβΫπ ’“φΙιΩΣΖΔ…ΧΥυ”–Θ§3ΡξΚσΟΩΡξΩ…ΜώΒΟΒΡΉβΫπΈΣ…ΧΤΧ±ξΦέΒΡ9%
Θ®1Θ©Έ ΆΕΉ ’Ώ―Γ‘ώΡΡ÷÷ΙΚΤΧΖΫΑΗΘ§5ΡξΚσΥυΜώΒΟΒΡΆΕΉ ’“φ¬ ΗϋΗΏΘΩΈΣ ≤Ο¥ΘΩ
Θ®ΉΔΘΚΆΕΉ ’“φ¬ =![]() ΓΝ100%Θ©
ΓΝ100%Θ©
Θ®2Θ©Ε‘Ά§“Μ±ξΦέΒΡ…ΧΤΧΘ§ΦΉ―Γ‘ώΝΥΙΚΤΧΖΫΑΗ“ΜΘ§““―Γ‘ώΝΥΙΚΤΧΖΫΑΗΕΰΘ§Ρ«Ο¥5ΡξΚσΝΫ»ΥΜώΒΟΒΡ ’“φœύ≤ν7.2Άρ‘ΣΘ°Έ ΦΉ““ΝΫ»ΥΗςΆΕΉ ΝΥΕύ…ΌΆρ‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥ΙΛ≥ß”κAΘ§BΝΫΒΊ”–ΙΪ¬ΖΓΔΧζ¬ΖœύΝ§.’βΦ“ΙΛ≥ߥ”AΒΊΙΚ¬ρ“Μ≈ζΟΩΕ÷1000‘ΣΒΡ‘≠Νœ‘ΥΜΊΙΛ≥ßΘ§÷Τ≥…ΟΩΕ÷8000‘ΣΒΡ≤ζΤΖ‘ΥΒΫBΒΊ.ΙΪ¬Ζ‘ΥΦέΈΣ1.5‘ΣΘ®Ε÷ΓΛ«ßΟΉΘ©Θ§Χζ¬Ζ‘ΥΦέΈΣ1.2‘ΣΘ®Ε÷ΓΛ«ßΟΉΘ©Θ§’βΝΫ¥Έ‘Υ δΙ≤÷ß≥ωΙΪ¬Ζ‘ΥΖ―15000‘ΣΘ§Χζ¬Ζ‘ΥΖ―97200‘Σ.’β≈ζ≤ζΤΖΒΡœζ έΩν±»‘≠ΝœΖ―”κ‘Υ δΖ―ΒΡΚΆΕύΕύ…Ό‘ΣΘΩΆΦ÷–ΚΎΑΉœύΦδΒΡœΏ±μ ΨΧζ¬ΖΘ§ΤδΥϋœΏ±μ ΨΙΪ¬Ζ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»Έ“β–¥≥ω“ΜΗω ΐΈΜ≤ΜΚ§ΝψΒΡ»ΐΈΜ ΐΘ§»Έ»Γ»ΐΗω ΐΉ÷÷–ΒΡΝΫΗωΘ§ΉιΚœ≥…Υυ”–Ω…ΡήΒΡΝΫΈΜ ΐΘ®”–6ΗωΘ©Θ§«σ≥ωΥυ”–’β–©ΝΫΈΜ ΐΒΡΚΆΘ§»ΜΚσΫΪΥϋ≥ΐ“‘‘≠»ΐΈΜ ΐΒΡΗςΗω ΐΈΜ…œΒΡ ΐΒΡΚΆ.άΐ»γΘ§Ε‘»ΐΈΜ ΐ223Θ§»ΓΤδΝΫΗω ΐΉ÷Ήι≥…Υυ”–Ω…ΡήΒΡΝΫΈΜ ΐΘΚ22Θ§23Θ§22Θ§23Θ§32Θ§32.ΥϋΟ«ΒΡΚΆ «154.»ΐΈΜ ΐ223ΗςΈΜ ΐΒΡΚΆ «7Θ§![]() ‘ΌΜΜΦΗΗω ΐ ‘“Μ ‘Θ§ΡψΖΔœ÷ΝΥ ≤Ο¥ΘΩ«κ–¥≥ωΡψΑ¥…œΟφΖΫΖ®ΒΡΧΫΥςΙΐ≥ΧΚΆΥυΖΔœ÷ΒΡΫαΙϊΘ§≤Δ‘Υ”Ο¥ζ ΐ ΫΒΡ÷Σ ΕΥΒΟςΥυΖΔœ÷ΒΡΫαΙϊΒΡ’ΐ»Ζ–‘.
‘ΌΜΜΦΗΗω ΐ ‘“Μ ‘Θ§ΡψΖΔœ÷ΝΥ ≤Ο¥ΘΩ«κ–¥≥ωΡψΑ¥…œΟφΖΫΖ®ΒΡΧΫΥςΙΐ≥ΧΚΆΥυΖΔœ÷ΒΡΫαΙϊΘ§≤Δ‘Υ”Ο¥ζ ΐ ΫΒΡ÷Σ ΕΥΒΟςΥυΖΔœ÷ΒΡΫαΙϊΒΡ’ΐ»Ζ–‘.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ΓœABC=90ΓψΘ§AB=3Θ§BC=4Θ§DC=12Θ§AD=13Θ§«σΥΡ±Ώ–ΈABCDΒΡΟφΜΐΘ°
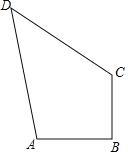
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() Θ§
Θ§![]() .
.

Θ®1Θ©”Ο≥ΏΙφΉςΆΦΖ®Ής![]() Θ§”κ±Ώ
Θ§”κ±Ώ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ®±ΘΝτΉςΧβΚέΦΘΘ§≤Μ”Ο–¥ΉςΖ®Θ©ΘΜ
Θ®±ΘΝτΉςΧβΚέΦΘΘ§≤Μ”Ο–¥ΉςΖ®Θ©ΘΜ
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§Β±![]() ±Θ§«σ
±Θ§«σ![]() ΒΡΕ» ΐ.
ΒΡΕ» ΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡψ÷ΣΒάΙ≈¥ζ ΐ―ßΦ“‘θ―υΫβ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ¬πΘΩ“‘x2©¹2x©¹3=0ΈΣάΐΘ§¥σ÷¬Ιΐ≥Χ»γœ¬ΘΚΒΎ“Μ≤ΫΘΚΫΪ‘≠ΖΫ≥Χ±δ–ΈΈΣx2©¹2x=3Θ§Φ¥xΘ®x©¹2Θ©=3Θ°
ΒΎΕΰ≤ΫΘΚΙΙ‘λ“ΜΗω≥ΛΈΣxΘ§ΩμΈΣΘ®x©¹2Θ©ΒΡ≥ΛΖΫ–ΈΘ§≥Λ±»Ωμ¥σ2Θ§«“ΟφΜΐΈΣ3Θ§»γΆΦΥυ ΨΘ°
ΒΎ»ΐ≤ΫΘΚ”ΟΥΡΗω’β―υΒΡ≥ΛΖΫ–ΈΈß≥…“ΜΗω¥σ’ΐΖΫ–ΈΘ§÷–Φδ «“ΜΗω–Γ’ΐΖΫ–ΈΘ§»γΆΦΥυ ΨΘ°
ΒΎΥΡ≤ΫΘΚΦΤΥψ¥σ’ΐΖΫ–ΈΟφΜΐ”Οx±μ ΨΈΣΓΓΓΓ ΓΓΓΓΘ°≥ΛΖΫ–ΈΟφΜΐΈΣ≥Θ ΐΓΓΓΓ Θ°–Γ’ΐΖΫ–ΈΟφΜΐΈΣ≥Θ ΐΓΓΓΓ Θ°
”…Ιέ≤λΩ…ΒΟΘ§¥σ’ΐΖΫ–ΈΟφΜΐΒ»”ΎΥΡΗω≥ΛΖΫ–Έ”κ–Γ’ΐΖΫ–ΈΟφΜΐ÷°ΚΆΘ§ΒΟΖΫ≥ΧΓΓΓΓ ΓΓΘ§ΝΫ±ΏΩΣΖΫΩ…«σΒΟΘΚx1=3Θ§x2=©¹1Θ°
Θ®1Θ©ΒΎΥΡ≤Ϋ÷–ΚαœΏ…œ”ΠΧν»κΓΓΓΓ ΓΓΓΓΘΜΓΓΓΓ ΓΓΓΓΘΜΓΓΓΓ ΓΓΓΓΘΜΓΓΓΓ ΓΓΓΓΘ°
Θ®2Θ©«κ≤ΈΩΦΙ≈»ΥΒΡΥΦΩΦΙΐ≥ΧΘ§Μ≠≥ω Ψ“βΆΦΘ§–¥≥ω≤Ϋ÷ηΘ§ΫβΖΫ≥Χx2©¹x©¹1=0Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com