
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形的圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).
(1)转动转盘一次,求转出的数字是﹣2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意可求得2个“-2”所占的扇形圆心角的度数,再利用概率公式进行计算即可得;
(2)由题意可得转出“1”、“3”、“-2”的概率相同,然后列表得到所有可能的情况,再找出符合条件的可能性,根据概率公式进行计算即可得.
(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,
∴转出的数字是﹣2的概率为![]() ;
;
(2)列表如下:
﹣2 | ﹣2 | 1 | 1 | 3 | 3 | |
﹣2 | 4 | 4 | ﹣2 | ﹣2 | ﹣6 | ﹣6 |
﹣2 | 4 | 4 | ﹣2 | ﹣2 | ﹣6 | ﹣6 |
1 | ﹣2 | ﹣2 | 1 | 1 | 3 | 3 |
1 | ﹣2 | ﹣2 | 1 | 1 | 3 | 3 |
3 | ﹣6 | ﹣6 | 3 | 3 | 9 | 9 |
3 | ﹣6 | ﹣6 | 3 | 3 | 9 | 9 |
由表可知共有36种等可能结果,其中数字之积为正数的有20种结果,
∴这两次分别转出的数字之积为正数的概率为![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,
上,![]() .点
.点![]() 为边
为边![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
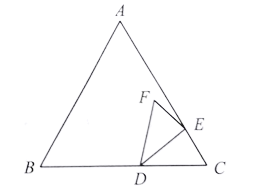
(1)当点![]() 在
在![]() 上时,求证:
上时,求证:![]() ;
;
(2)当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(3)连接![]() 设
设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 记
记![]()
![]() 是否存在最大值?若存在,请直接写出
是否存在最大值?若存在,请直接写出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点![]() 、
、![]() 、
、![]() 、
、![]() 分别是“果圆”与坐标轴的交点,抛物线的解析式为
分别是“果圆”与坐标轴的交点,抛物线的解析式为![]() ,
,![]() 为半圆的直径,则这个“果圆”被
为半圆的直径,则这个“果圆”被![]() 轴截得的弦
轴截得的弦![]() 的长为_________.
的长为_________.
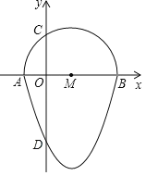
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,在边
的中点,在边![]() 上取点
上取点![]()
![]() ,点
,点![]() 在边
在边![]() 上,且满足
上,且满足![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() ,
,![]() 将
将![]() 分割成I、II、III、IV四个部分,将这四个部分重新拼接可以得到如图2所示的矩形
分割成I、II、III、IV四个部分,将这四个部分重新拼接可以得到如图2所示的矩形![]() ,若
,若![]() ,则图1中
,则图1中![]() 的长为_______.
的长为_______.
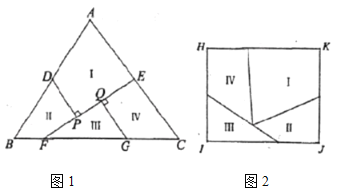
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值____.
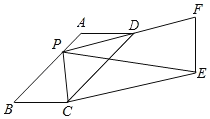
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
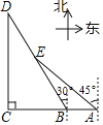
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com