
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4.
(1)求抛物线的表达式;
(2)求∠CAB的正切值;
(3)如果点P是x轴上的一点,且∠ABP=∠CAO,直接写出点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)![]() ;(3)点P的坐标是(1,0)
;(3)点P的坐标是(1,0)
【解析】
(1) 先求得抛物线的对称轴方程, 然后再求得点C的坐标,设抛物线的解析式为y=a(x+1)2+4,将点 (-3, 0) 代入求得a的值即可;
(2) 先求得A、 B、 C的坐标, 然后依据两点间的距离公式可得到BC、AB,AC的长,然后依据勾股定理的逆定理可证明∠ABC=90°,最后,依据锐角三角函数的定义求解即可;
(3) 连接BC,可证得△AOB是等腰直角三角形,△ACB∽△BPO,可得![]() 代入个数据可得OP的值,可得P点坐标.
代入个数据可得OP的值,可得P点坐标.
解:(1)由题意得,抛物线y=ax2+2ax+c的对称轴是直线![]() ,
,
∵a<0,抛物线开口向下,又与x轴有交点,
∴抛物线的顶点C在x轴的上方,
由于抛物线顶点C到x轴的距离为4,因此顶点C的坐标是(﹣1,4).
可设此抛物线的表达式是y=a(x+1)2+4,
由于此抛物线与x轴的交点A的坐标是(﹣3,0),可得a=﹣1.
因此,抛物线的表达式是y=﹣x2﹣2x+3.
(2)如图1,
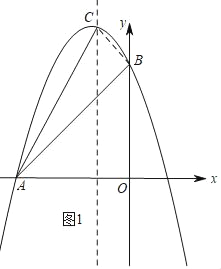
点B的坐标是(0,3).连接BC.
∵AB2=32+32=18,BC2=12+12=2,AC2=22+42=20,
得AB2+BC2=AC2.
∴△ABC为直角三角形,∠ABC=90°,
所以tan∠CAB=![]() .
.
即∠CAB的正切值等于![]() .
.
(3)如图2,连接BC,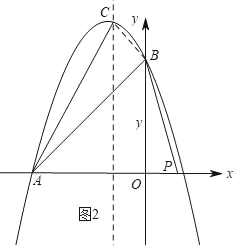
∵OA=OB=3,∠AOB=90°,
∴△AOB是等腰直角三角形,
∴∠BAP=∠ABO=45°,
∵∠CAO=∠ABP,
∴∠CAB=∠OBP,
∵∠ABC=∠BOP=90°,
∴△ACB∽△BPO,
∴![]() ,
,
∴![]() ,OP=1,
,OP=1,
∴点P的坐标是(1,0).


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
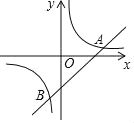
【题目】如图,一次函数y=kx+b(k≠0)和反比例函数y=![]() (m≠0)分别交于点A(4,1),B(﹣1,a)
(m≠0)分别交于点A(4,1),B(﹣1,a)
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出kx+b>![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy内有三点:(0,﹣2),(1,﹣1),(2.17,0.37).则过这三个点_____(填“能”或“不能”)画一个圆,理由是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
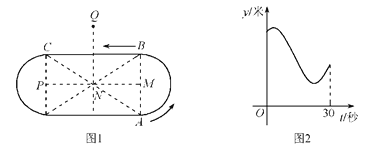
A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
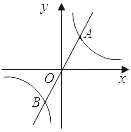
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
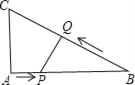
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com