
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
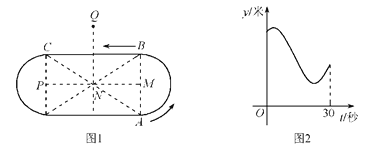
A. 点M B. 点N C. 点P D. 点Q
【答案】D
【解析】
动点问题的函数图象.
分别在点M、N、P、Q的位置,结合函数图象进行判断,利用排除法即可得出答案:
A、在点M位置,则从A至B这段时间内,弧![]() 上每一点与点M的距离相等,即y不随时间的变化改变,与函数图象不符,故本选项错误;
上每一点与点M的距离相等,即y不随时间的变化改变,与函数图象不符,故本选项错误;
B、在点N位置,则根据矩形的性质和勾股定理,NA=NB=NC,且最大,与函数图象不符,故本选项错误;
C、在点P位置,则PC最短,与函数图象不符,故本选项错误;
D、在点P位置,如图所示,①以Q为圆心,QA为半径画圆交![]() 于点E,其中y最大的点是AE的中垂线与弧
于点E,其中y最大的点是AE的中垂线与弧![]() 的交点H;②在弧
的交点H;②在弧![]() 上,从点E到点C上,y逐渐减小;③QB=QC,即
上,从点E到点C上,y逐渐减小;③QB=QC,即![]() ,且BC的中垂线QN与BC的交点F是y的最小值点。经判断点Q符合函数图象,故本选项正确。
,且BC的中垂线QN与BC的交点F是y的最小值点。经判断点Q符合函数图象,故本选项正确。
故选D。


科目:初中数学 来源: 题型:
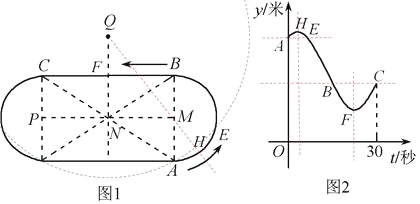
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
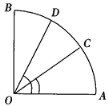
【题目】已知:如图,∠AOB=90°,AO=OB,C、D是弧AB上的两点,∠AOD>∠AOC,
(1)0<sin∠AOC<sin∠AOD<1;
(2)1>cos∠AOC>cos∠AOD>0;
(3)锐角的正弦函数值随角度的增大而______;
(4)锐角的余弦函数值随角度的增大而______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4.
(1)求抛物线的表达式;
(2)求∠CAB的正切值;
(3)如果点P是x轴上的一点,且∠ABP=∠CAO,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,正方形ABCD和一个圆心角为45°的扇形,圆心与A点重合,此扇形绕A点旋转时,两半径分别交直线BC、CD于点P.K.
(1)当点P、K分别在边BC.CD上时,如图(1),求证:BP+DK=PK.
(2)当点P、K分别在直线BC.CD上时,如图(2),线段BP、DK、PK之间又有怎样的数量关系,请直接写出结论.
(3)在图(3)中,作直线BD交直线AP、AK于M、Q两点.若PK=5,CP=4,求PM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
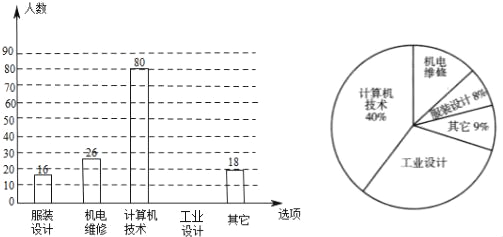
【题目】每年5月的第二周为“职业教育活动周”,今年我省开展了以“弘扬工匠精神,打造技能强国”为主题的系列活动.活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校教务处随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).请解答以下问题:
(1)补全条形统计图和扇形统计图;
(2)若该校共有1800名学生,请估计该校对“工业设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中,随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
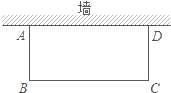
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com