
【题目】已知:如图,∠AOB=90°,AO=OB,C、D是弧AB上的两点,∠AOD>∠AOC,
(1)0<sin∠AOC<sin∠AOD<1;
(2)1>cos∠AOC>cos∠AOD>0;
(3)锐角的正弦函数值随角度的增大而______;
(4)锐角的余弦函数值随角度的增大而______.
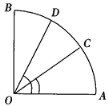
【答案】(1)见解析(2)见详解;(3)增大;(4)减小.
【解析】
第(1)(2)问作辅助线,分别在Rt△OEC和Rt△DFO中利用三角函数定义表示出所求三角函数,再利用不等式的性质:不等号两边同时除以同一个不为零的正数时不等号仍成立即可解题;第(3)(4)两问根据特殊三角函数值,总结规律即可解题.
解:(1)如图所示,作CE⊥OA与E,作DF⊥OA与F.
∵sin∠AOC=![]() , sin∠AOD=
, sin∠AOD=![]() ,
,![]() ,
,
∴0<sin∠AOC<sin∠AOD<1;(不等式性质)
(2)∵cos∠AOC=![]() , cos∠AOD=
, cos∠AOD=![]() ,
,![]() ,
,
∴1>cos∠AOC>cos∠AOD>0;(不等式性质)
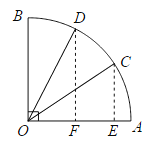
(3)由特殊的直角三角函数值,总结规律,即可发现对于锐角而言, 锐角的正弦函数值随角度的增大而增大;
(4)由特殊的直角三角函数值,总结规律,即可发现对于锐角而言, 锐角的余弦函数值随角度的增大而减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
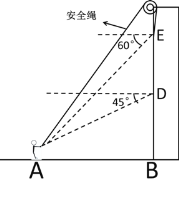
【题目】《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动。某学校组织了一次户外攀岩活动,如图,攀岩墙体近似看作垂直于地面,一学生攀到D点时,距离地面B点3.6米,该学生继续向上很快就攀到顶点E。在A处站立的带队老师拉着安全绳,分别在点D和点E测得点C的俯角是45°和60°,带队老师的手C点距离地面1.6米,请求出攀岩的顶点E距离地面的高度为多少米?(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全
班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
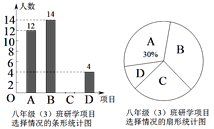
(1)八年级(3)班学生总人数是多少,并将条形统计图补充完整;
(2)宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;
(3)若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
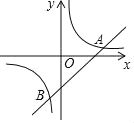
【题目】如图,一次函数y=kx+b(k≠0)和反比例函数y=![]() (m≠0)分别交于点A(4,1),B(﹣1,a)
(m≠0)分别交于点A(4,1),B(﹣1,a)
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出kx+b>![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
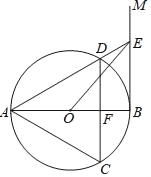
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,点A,C,D分别为⊙O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
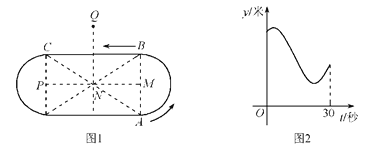
A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别画有正三角形、平行四边形、菱形图案的卡片,它们除图案外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的每一张卡片的图案既是轴对称图形又是中心对称图形的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆上有A、B、C三点,直线l与圆相切于点A,CD平分∠ACB,且与l交于点D,若![]() =80°,
=80°,![]() =60°,则∠ADC的度数为( )
=60°,则∠ADC的度数为( )
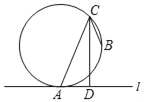
A. 80° B. 85° C. 90° D. 95°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com