
【题目】如图,已知,正方形ABCD和一个圆心角为45°的扇形,圆心与A点重合,此扇形绕A点旋转时,两半径分别交直线BC、CD于点P.K.
(1)当点P、K分别在边BC.CD上时,如图(1),求证:BP+DK=PK.
(2)当点P、K分别在直线BC.CD上时,如图(2),线段BP、DK、PK之间又有怎样的数量关系,请直接写出结论.
(3)在图(3)中,作直线BD交直线AP、AK于M、Q两点.若PK=5,CP=4,求PM的长.

【答案】(1)证明见解析;(2)BP=DK+PK,理由见解析;(3)PM的长是![]() .
.
【解析】
(1)延长CD到N,使DN=BP,连接AN,根据正方形的性质和全等三角形的判定SAS证△ABP≌△ADN,推出AN=AP,∠NAD=∠PAB,求出∠NAK=∠KAP=45°,根据SAS证△NAK和△KAP全等即可;
(2)在BC上截取BN=DK,连接AN,与(1)类似证△ADK≌△ABN和△KAP≌△NAP,推出BN=DK,NP=PK即可;
(3)在DC上截取DN=BP,连接AN,与(1)类似证△ADN≌△ABP和△KAP≌△KAN,推出BP=DN,NK=PK,得出DK=PB+PK,求出正方形的边长,根据勾股定理求出AN、AK、AP,求出∠ABM=∠ACK=135°,∠PAB=∠CAK,证△MAB和△KAC相似,得出比例式,代入求出即可.
(1)证明:延长CD到N,使DN=BP,连接AN,
∵正方形ABCD,
∴∠ABP=∠ADC=90°=∠BAD,AD=AB,
∴∠ADN=90°=∠ABP,
在△ABP和△ADN中
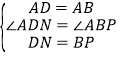 ,
,
∴△ABP≌△ADN,
∴AN=AP,∠NAD=∠PAB,
∵∠BAD=90°,∠PAK=45°,
∴∠BAP+∠KAD=45°,
∴∠NAD+∠DAK=45°,
即∠NAK=∠KAP=45°,
在△NAK和△KAP中
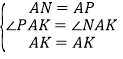 ,
,
∴△PAK≌△NAK,
∴NK=KP,
∴BP+DK=PK.
(2)解:BP=DK+PK,
理由是:在BC上截取BN=DK,连接AN,
与(1)类似△ADK≌△ABN,
∴AK=AN,∠KAD=∠BAN,
∵∠KAP=45°,
∴∠NAB+∠DAP=45°,
∴∠NAP=90°﹣45°=45°=∠KAP,
与(1)类似△KAP≌△NAP(SAS),
∴PK=PN,
∴BP=BN+NP=DK+PK,
即BP=DK+PK.
(3)解:在△CPK中,CP=4,PK=5,由勾股定理得:CK=3,
在DC上截取DN=BP,连接AN,
由(1)可知:AN=AP,
与(2)证法类似△NAK≌△PAK,
∴PK=NK,
∴DK=PB+PK,
即DC+3=4﹣BC+5,
∵正方形ABCD,DC=BC,
解得:AD=DC=BC=AB=3,
连接AC,
∵正方形ABCD,
∴∠ACB=∠DBC=∠MBP=45°,
∵∠ABC=∠PCK=90°,
∴∠ABM=∠ACK=45°+90°=135°,
在Rt△ABC中,由勾股定理得:AC=3![]() ,
,
在Rt△ABP中,由勾股定理得:AP=![]() =
=![]() ,
,
在Rt△ADK中,由勾股定理得:AK=![]() =3
=3![]() ,
,
∵∠PAK=∠BAC=45°,∠BAK=∠BAK,
∴∠PAB=∠KAC,
∵∠ABM=∠ACK,
∴△MAB∽△KAC,
∴![]() ,
,
即![]() =
=![]() ,
,
解得:PM=![]() ,
,
答:PM的长是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全
班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
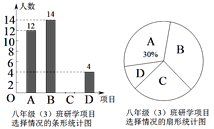
(1)八年级(3)班学生总人数是多少,并将条形统计图补充完整;
(2)宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;
(3)若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
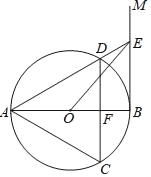
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,点A,C,D分别为⊙O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
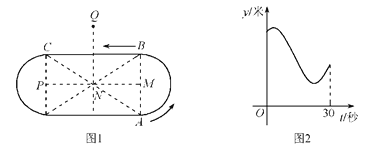
A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别画有正三角形、平行四边形、菱形图案的卡片,它们除图案外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的每一张卡片的图案既是轴对称图形又是中心对称图形的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一张简易活动餐桌,测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌脚的张角∠COD的度数大小应为( )
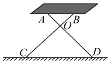
A. 100° B. 120° C. 135° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com