
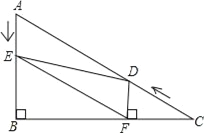
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬BC=5![]() ����C=30������D�ӵ�C������CA������ÿ��2����λ�����ٶ���A�������˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ�����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��
����C=30������D�ӵ�C������CA������ÿ��2����λ�����ٶ���A�������˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ�����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��
��1��AC�ij������� ��AB�ij����� ��
��2����D��E���˶������У��߶�EF��AD�Ĺ�ϵ�Ƿ����仯�������仯����ô�߶�EF��AD�Ǻι�ϵ��������֤�������仯����˵�����ɣ�
��3����tΪ��ֵ����BEF�������2![]() ��
��
���𰸡���1��10��5����2��EF��ADƽ������ȣ���3��3.
��������������(1)�����ݺ���30��ǵ�ֱ�������ε������Լ�BC�ij������AC��AB�ij��ȣ�(2)�������˶����ٶȵó�AE=DF�����ݴ�ֱ�ó�AE��DF���Ӷ��ó��ı���AEFDΪƽ���ı��Σ��Ӷ��ó�EF��AD�Ĺ�ϵ��(3)�������˶����ٶ��ú�t�Ĵ���ʽ��ʾBE��BF�ij��ȣ�Ȼ�����ֱ�������ε�������㷨��ó�t��ֵ��
��⣺��1���⣺����Rt��ABC�У���C=30�㣬 ��AC=2AB��
���ݹ��ɶ����ã�AC2��AB2=BC2�� ��3AB2=75�� ��AB=5��AC=10��
��2��EF��ADƽ������ȣ�
֤��������DFC�У���DFC=90�㣬��C=30�㣬DC=2t�� ��DF=t�� �֡�AE=t��
��AE=DF�� ��AB��BC��DF��BC�� ��AE��DF��
���ı���AEFDΪƽ���ı��Σ� ��EF��ADƽ������ȣ�
��3���⣺����Rt��CDF�У���A=30�㣬 ��DF=![]() CD�� ��CF=
CD�� ��CF=![]() t��
t��
�֡�BE=AB��AE=5��t��BF=BC��CF=5![]() ��
��![]() t��
t��
��![]() �� ����
�� ����![]() ��
��
��ã�t=3��t=7������������ȥ���� ��t=3��
�ʵ�t=3ʱ����BEF�����Ϊ2![]() ��
��


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƿ�ƾ�����ƿ��![]() ����Ũ��δ֪����ƿ��
����Ũ��δ֪����ƿ��![]() ����Ũ��
����Ũ��![]() ���Ӽ�ƿ�е�����ƿ
���Ӽ�ƿ�е�����ƿ![]() ���ƾ���ҡ�Ⱥ�һ���ָ���ƿ����ʱ��ƿŨ��Ϊ
���ƾ���ҡ�Ⱥ�һ���ָ���ƿ����ʱ��ƿŨ��Ϊ![]() ����ƿŨ��Ϊ
����ƿŨ��Ϊ![]() ����ʱ��ƿ���оƾ��� ������
����ʱ��ƿ���оƾ��� ������
A. 5 B. 6.3 C. 5.25 D. 5.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ϊ���������븺��������
���ɻ���ǰ�˶�![]() ǧ����
ǧ����![]() ǧ�ף��������˶�
ǧ�ף��������˶�![]() ǧ����
ǧ����![]() ǧ�ף�
ǧ�ף�
���������Ȼ����������������![]() ���Ǹ��������Ƿ�����������ȷ���У� ��
���Ǹ��������Ƿ�����������ȷ���У� ��
A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У�ABΪ��O��ֱ����AB=4������P��A���������ÿ��и���λ���ٶ��ڡ�O�ϰ�˳ʱ�뷽���˶�һ�ܣ��趯��P���˶�ʱ��Ϊt�룬��C��Բ����һ�㣬�ҡ�AOC=40�㣬��t=��ʱ����P���C���ĶԳƣ��ҶԳ�������ֱ��AB�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�ܳ�2.5m������ABб����ǽAC�ϣ���C=90������ʱ�����ӵĵ�B��ǽ��C�ľ���BCΪ0.7m��
��1�����ʱ���ӵĶ���A�����ĸ߶�AC��
��2��������ӵĶ���A�»���0.9m����ô���ӵĶ���B��ˮƽ���������һ����˶�Զ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC��AEƽ����BAC����B=70������C=30������
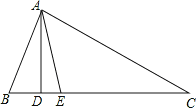
��1����BAE�Ķ�����
��2����DAE�Ķ�����
��3��̽����С����Ϊ���������B=70������C=30���ij���B-��C=40����Ҳ�ܵó���DAE�Ķ��������ܣ�����д�������̣������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ����Բ�������ߵ�һ������ɵķ��ͼ�γ�Ϊ����Բ����
��ͼ��������y=x2��2x��3��x�ύ�ڵ�A��B����y�ύ�ڵ�D����ABΪֱ������x���Ϸ�����Բ��y���ڵ�C����Բ��Բ�ļ�ΪM����ʱ�����Բ������������x���·�������ɵ�ͼ�ξͳ�Ϊ����Բ����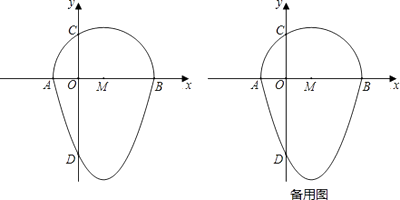
��1��ֱ��д����A��B��C�����꼰����Բ����CD�ij���
A �� B �� C �� CD=��
��2�����һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ�
������C�ġ���Բ�����ߵĽ���ʽ��
������D�ġ���Բ�����ߵĽ���ʽ��
��3���ɣ�2����ù���D�ġ���Բ��������x�ύ���ΪE����F�ǡ���Բ����һ���㣬�����Ƿ����S��CDE=S��CDF �� �������������F�����ꣻ�������ڣ���˵�����ɣ�
��4����P�ǡ���Բ����һ�㣬�������BPC=60�㣬��BP���ʱ����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����һ�Σ�
����![]()
�۲췢�֣���ʽ�ӵڶ�����ÿ�����ǰ��һ���![]() �����������ʽ�������
�����������ʽ�������![]() ����������ʽ�г��������⣬������ԭʽ�е�����ͬ��������ʽ�����ʹ�����ڼ��㣮
����������ʽ�г��������⣬������ԭʽ�е�����ͬ��������ʽ�����ʹ�����ڼ��㣮
�⣺��![]() ����
����
��![]() ����
����
��-�ٵ�![]() ����
����![]() ��
��
��������õķ�����Ϊ����λ������������һ�������ӵڶ�����ÿһ����ǰһ��֮�ȶ���ȣ��������Ƕ�����![]() ������ô��������������⣬��������������λ��������������
������ô��������������⣬��������������λ��������������
��������۲���ʽ![]() �Ƿ�߱��������ɣ����ǣ����㳢��������λ�������������ʽ�Ľ����
�Ƿ�߱��������ɣ����ǣ����㳢��������λ�������������ʽ�Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y= ![]() ��ͼ����һ�κ���y=kx+b��ͼ����A��B���㣬��A������Ϊ��2��6������B������Ϊ��n��1����
��ͼ����һ�κ���y=kx+b��ͼ����A��B���㣬��A������Ϊ��2��6������B������Ϊ��n��1���� 
��1������������һ�κ����ı���ʽ��
��2����EΪy����һ�����㣬��S��AEB=10�����E�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com