
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
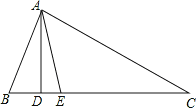
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
【答案】(1) 40°;(2) 20°;(3)能,20°.
【解析】
试题分析:(1)根据三角形内角和定理得∠BAC=180°-∠B-∠C=80°,然后根据角平分线定义得∠BAE=![]() ∠BAC=40°;
∠BAC=40°;
(2)由于AD⊥BC,则∠ADE=90°,根据三角形外角性质得∠ADE=∠B+∠BAD,所以∠BAD=90°-∠B=20°,然后利用∠DAE=∠BAE-∠BAD进行计算;
(3)根据三角形内角和定理得∠BAC=180°-∠B-∠C,再根据角平分线定义得∠BAE=![]() ∠BAC=
∠BAC=![]() (180°-∠B-∠C)=90°-
(180°-∠B-∠C)=90°-![]() (∠B+∠C),加上∠ADE=∠B+∠BAD=90°,则∠BAD=90°-∠B,然后利用角的和差得∠DAE=∠BAE-∠BAD=90°-
(∠B+∠C),加上∠ADE=∠B+∠BAD=90°,则∠BAD=90°-∠B,然后利用角的和差得∠DAE=∠BAE-∠BAD=90°-![]() (∠B+∠C)-(90°-∠B)=
(∠B+∠C)-(90°-∠B)=![]() (∠B-∠C),即∠DAE的度数等于∠B与∠C差的一半.
(∠B-∠C),即∠DAE的度数等于∠B与∠C差的一半.
试题解析:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=40°;
∠BAC=40°;
(2)∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-70°=20°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°;
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°-∠B-∠C)=90°-
(180°-∠B-∠C)=90°-![]() (∠B+∠C),
(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-![]() (∠B+∠C)-(90°-∠B)=
(∠B+∠C)-(90°-∠B)=![]() (∠B-∠C),
(∠B-∠C),
∵∠B-∠C=40°,
∴∠DAE=![]() ×40°=20°.
×40°=20°.


科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,对自来水用户按用水量分段收费:若每月用水不超过![]() 吨,按每吨
吨,按每吨![]() 元收费;若每月用水超过
元收费;若每月用水超过![]() 吨,则超过
吨,则超过![]() 吨的部分按每吨
吨的部分按每吨![]() 元收费,其余部分仍按
元收费,其余部分仍按![]() 元收费.
元收费.
![]() 若该市某户居民某月用水
若该市某户居民某月用水![]() 吨,问:该户居民应交水费多少元?
吨,问:该户居民应交水费多少元?
![]() 若该市某户居民
若该市某户居民![]() 月份交水费
月份交水费![]() 元,问:该户居民
元,问:该户居民![]() 月份的用水量是多少吨?
月份的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级进行数学竞赛,在第二环节的10道题中,答对1题得10分,答错一题扣5分,不答不得分,二班实际得分![]() 分,则下列选项正确的是( )
分,则下列选项正确的是( )
A. 答对1题,答错5题,不答4题 B. 答对2题,答错5题,不答3题
C. 答对2题,答错5题,不答3题 D. 答对4题,答错5题,不答1题
查看答案和解析>>
科目:初中数学 来源: 题型:
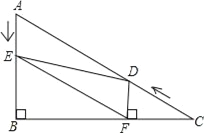
【题目】如图,在Rt△ABC中,∠B=90°,BC=5![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)当t为何值,△BEF的面积是2![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)![]() 的解集是
的解集是
(3)![]() 的解集是
的解集是
(4)![]() 的解集是
的解集是
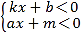
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一份汽车票价表,李丽星期一、三、五要乘汽车上下班,星期二、四乘汽车上班,而搭朋友的车回家;她应该买什么样的票合算?如果周末她要乘汽车去公园,那么她选哪种票合算?
汽车公司票价表
单程票 |
|
周票 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com