
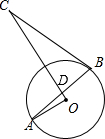
 AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.
AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.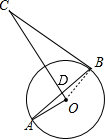


科目:初中数学 来源: 题型:
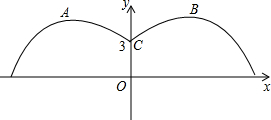 如图,一盆君子兰花的两片绿叶是形状相同的抛物线,它们的交接处距花土面3cm,两片绿叶最高点之间的距离是12cm,最高点到花土面的距离是4.2m,分别求出左、右两边抛物线的解析式.
如图,一盆君子兰花的两片绿叶是形状相同的抛物线,它们的交接处距花土面3cm,两片绿叶最高点之间的距离是12cm,最高点到花土面的距离是4.2m,分别求出左、右两边抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
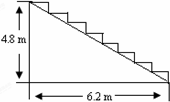 遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要
遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com