
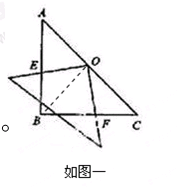
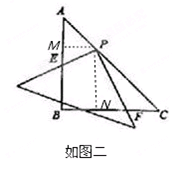
 , ∴BF=
, ∴BF=
 , ∴BF=0
, ∴BF=0 ,
,

科目:初中数学 来源:不详 题型:解答题



 的大小关系.
的大小关系.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠
的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠 次后所得到的等腰直角三角形(如图n+1)的斜边长为( * ).
次后所得到的等腰直角三角形(如图n+1)的斜边长为( * ).
A. | B. | C.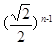 | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A.2 | B.3 | C. | D.1+ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的场地,长
的场地,长 ,宽
,宽 ,从
,从 、
、 两处入口的中路宽都为
两处入口的中路宽都为 ,两小路汇合处路宽为
,两小路汇合处路宽为 ,其余部分种植草坪,则草坪面积为( )
,其余部分种植草坪,则草坪面积为( )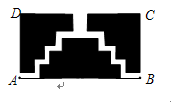
| A.5050m² | B.5000m² | C.4900m² | D.4998m² |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com