

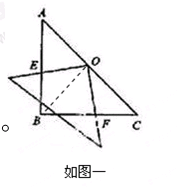
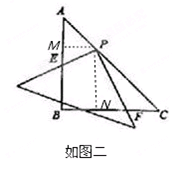
 (MN最短就是AB一半,最长就是AB中点到C距离)
(MN最短就是AB一半,最长就是AB中点到C距离) ,
, ,
, =
= 
 =12+4
=12+4 .
.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,四边形
,四边形 的四个顶点都在格点上,
的四个顶点都在格点上, 为
为 边的中点,若把四边形
边的中点,若把四边形 绕着点
绕着点 顺时针旋转
顺时针旋转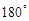 .
. 旋转后的图形;
旋转后的图形; 旋转后的对应点为
旋转后的对应点为 ,则
,则 ;
; 在旋转过程中所经过的路径长.
在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.等腰三角形 | B.正三角形 | C.菱形 | D.等腰梯形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 得到正方形
得到正方形 ,如图1所示.
,如图1所示. =45
=45 时(如图2),若线段
时(如图2),若线段 与边
与边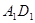 的交点为
的交点为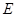 ,线段
,线段 与
与 的交点为
的交点为 ,可得下列结论成立 ①
,可得下列结论成立 ① ;②
;② ,试选择一个证明.
,试选择一个证明.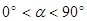 时,第(1)小题中的结论
时,第(1)小题中的结论 还成立吗?如果成立,请证明;如果不成立,请说明理由
还成立吗?如果成立,请证明;如果不成立,请说明理由 与AB边相交于P,Q两点,探究
与AB边相交于P,Q两点,探究 的度数是否发生变化?如果变化,请描述它与
的度数是否发生变化?如果变化,请描述它与 之间的关系;如果不变,请直接写出
之间的关系;如果不变,请直接写出 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.①② | B.②③ | C.②④ | D.①④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com