
 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.
将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.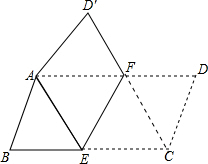 证明:(1)∵平行四边形纸片ABCD折叠,使点C与A重合,点D落到D′处,折痕为EF,
证明:(1)∵平行四边形纸片ABCD折叠,使点C与A重合,点D落到D′处,折痕为EF,
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
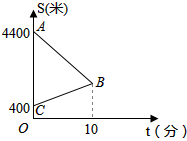 某天,小明来到体育馆看球赛,在距离体育场400米处的超市买水时发现门票还在家里,此时离比赛开始还有20分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他4倍的速度给他送票,两人在途中相遇后,小明立即以原步行速度的1.2倍赶回体育馆.如图中线段AB、BC分别表示父子送票、儿子取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题:
某天,小明来到体育馆看球赛,在距离体育场400米处的超市买水时发现门票还在家里,此时离比赛开始还有20分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他4倍的速度给他送票,两人在途中相遇后,小明立即以原步行速度的1.2倍赶回体育馆.如图中线段AB、BC分别表示父子送票、儿子取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
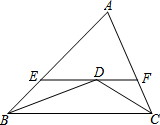 如图,已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,AB=8cm,AC=6cm.
如图,已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,AB=8cm,AC=6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com