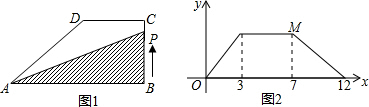
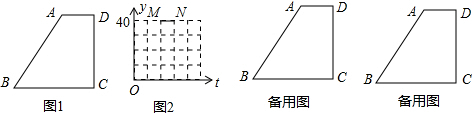
解:(1)如图1.设动点P出发t秒后,点P到达点A且点Q正好到达点C时,BC=BA=t,
则S
△BPQ=

BC•CD=

×t×8=40,
所以t=10(秒),
则BC=BA=10cm,点M的坐标为(10,40).
过点A作AH⊥BC于H,则四边形AHCD是矩形,
∴AD=CH,CD=AH=8cm,
在Rt△ABH中,∵∠AHB=90°,AB=10cm,AH=8cm,
∴BH=

=6cm,
∴CH=BC-BH=4cm,
∴AD=4cm;

(2)如备用图1,延长AD到A′,使A′D=AD,连接A′B,交CD于P,
则PA+PB=PA′+PB=A′B最小.
∵A′D∥BC,
∴△A′DP∽△BCP,
∴
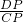
=
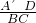
,即
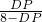
=
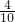
,
解得DP=

,
∴BA+AD+DP=10+4+

=
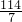
,
∴t=
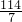
÷1=
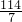
.
故P在CD边上运动时,存在时刻t=
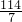
秒,能够使△PAB的周长最小;
(3)△PCD为等腰三角形时,分三种情况:
①如果PC=PD,如备用图2,作CD的垂直平分线交AB于P
1,则P
1为AB的中点,此时t
1=BP
1÷1=5;
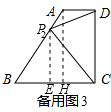
②如果CP=CD=8,如备用图3,以C为圆心,CD长为半径画弧,交AB于点P
2,过P
2作P
2E⊥BC于E,过点A作AH⊥BC于H.
设BP
2=x,则P
2E=BP
2•sin∠B=x•

=

x,BE=BP
2•cos∠B=

x,
∴CE=BC-BE=10-

x.
在Rt△P
2EC中,∵∠P
2EC=90°,
∴P
2E
2+CE
2=CP
22,(

x)
2+(10-

x)
2=64,
整理,得x
2-12x+36=0,
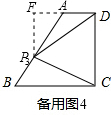
解得x
1=x
2=6,
∴BP
2=6,t
2=BP
2÷1=6;
③如果DP=DC,如备用图4,以D为圆心,CD长为半径画弧,交AB于点P
3,过P
3作P
3F⊥AD于F.
设AP
3=y,则P
3F=AP
3•sin∠FAP
3=AP
3•sin∠B=y•

=

y,AF=AP
3•cos∠B=

y,
∴DF=DA+AF=4+

y.
在Rt△P
3FD中,∵∠P
3FD=90°,
∴P
3F
2+DF
2=DP
32,(

y)
2+(4+

y)
2=64,
整理,得5y
2+24y-240=0,
解得y
1=
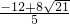
,y
2=
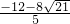
(不合题意舍去),
∴BP
3=AB-AP
3=10-
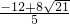
=
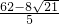
,t
3=BP
3÷1=
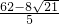
;
综上所述,△PCD能成为等腰三角形,此时t的值为5秒或6秒或
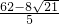
秒;
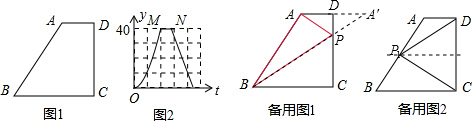
(4)当点P在BA边上时,
y=

×t×tsinB=

t
2×

=

t
2(0≤t≤10);
当点P在DC边上时,
y=

×10×(22-t)=-5t+110(14≤t≤22);
如图2所示.
分析:(1)P在AD边上运动时,△BPQ以BQ为底边,以CD长为高,因此可根据△BPQ的面积为40cm
2求出BC=10cm,而P、Q速度相同,P到A的时间与Q到C的时间相同,因此BA=BC=10cm,点M的坐标为(10,40).求AD的长可通过构建直角三角形来求解.过A作AH⊥BC与H,那么在直角三角形ABH中,AH=CD=8cm,BA=10cm,因此可根据勾股定理求出BH=6cm,那么AD=BC-BH=4cm;
(2)△PAB的周长=PA+AB+PB,而AB=10cm为定值,所以当PA+PB最小时,△PAB的周长最小.延长AD到A′,使A′D=AD,连接A′B,交CD于P,此时PA+PB最小.由△A′DP∽△BCP,根据相似三角形对应边成比例即可求解;
(3)△PCD为等腰三角形时,分三种情况进行讨论:①PC=PD;②CP=CD;③DP=DC;
(4)△BQP中,BQ=t,BP=t,以BQ为底边的高可用BP•sin∠B来表示,然后可根据三角形的面积计算公式得出关于y,t的函数关系式.
点评:本题是四边形综合题,主要考查了梯形的性质,三角形的面积,解直角三角形,相似三角形的判定与性质,轴对称-最短路线,等腰三角形的性质等知识,综合性较强,有一定难度.借助函数图象表达题目中的信息,读懂图象是关键.

 BC•CD=
BC•CD= ×t×8=40,
×t×8=40, =6cm,
=6cm, (2)如备用图1,延长AD到A′,使A′D=AD,连接A′B,交CD于P,
(2)如备用图1,延长AD到A′,使A′D=AD,连接A′B,交CD于P,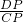 =
=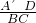 ,即
,即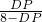 =
=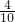 ,
, ,
, =
=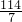 ,
,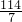 ÷1=
÷1=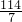 .
.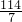 秒,能够使△PAB的周长最小;
秒,能够使△PAB的周长最小; ②如果CP=CD=8,如备用图3,以C为圆心,CD长为半径画弧,交AB于点P2,过P2作P2E⊥BC于E,过点A作AH⊥BC于H.
②如果CP=CD=8,如备用图3,以C为圆心,CD长为半径画弧,交AB于点P2,过P2作P2E⊥BC于E,过点A作AH⊥BC于H. =
= x,BE=BP2•cos∠B=
x,BE=BP2•cos∠B= x,
x, x.
x. x)2+(10-
x)2+(10- x)2=64,
x)2=64, 解得x1=x2=6,
解得x1=x2=6, =
= y,AF=AP3•cos∠B=
y,AF=AP3•cos∠B= y,
y, y.
y. y)2+(4+
y)2+(4+ y)2=64,
y)2=64,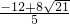 ,y2=
,y2=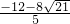 (不合题意舍去),
(不合题意舍去),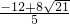 =
=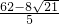 ,t3=BP3÷1=
,t3=BP3÷1=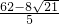 ;
;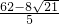 秒;
秒; (4)当点P在BA边上时,
(4)当点P在BA边上时, ×t×tsinB=
×t×tsinB= t2×
t2× =
= t2(0≤t≤10);
t2(0≤t≤10); ×10×(22-t)=-5t+110(14≤t≤22);
×10×(22-t)=-5t+110(14≤t≤22);

 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )