
分析 (1)分m=0与m≠0两种情况进行讨论即可;
(2)令y=0,则 mx2+(3m+1)x+3=0,求出x的值,再由抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数得出m的值,代入抛物线的解析式即可;
(3)把点P(x1,y1)与Q(x1+n,y2)代入抛物线的解析式,根据y1=y2可得出2x1=-n-4,代入代数式进行计算即可.
解答 解:(1)当m=0时,原方程化为x+3=0,
此时方程有实数根x=-3.
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2≥0,
∴此时方程有两个实数根.
综上,不论m为任何实数时,方程mx2+(3m+1)x+3=0总有实数根.
(2)∵令y=0,则 mx2+(3m+1)x+3=0.
解得x1=-3,x2=-$\frac{1}{m}$.
∵抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,
∴m=1.
∴抛物线的解析式为y=x2+4x+3.
(3)∵点P(x1,y1)与Q(x1+n,y2)在抛物线上,
∴y1=x12+4x1+3,y2=(x1+n)2+4(x1+n)+3,
∵y1=y2,
∴x12+4x1+3=(x1+n)2+4(x1+n)+3,
可得n(2x1+n+4)=0.
∵点P,Q不重合,
∴n≠0.
∴2x1=-n-4.
∴4x12+12x1n+5n2+16n+2000=(2x1)2+2x1-6n+5n2+16n+2000=(n+4)2+6n(-n-4)+5n2+16n+2000=2016.
点评 本题考查的是抛物线与x轴的交点,在解答(1)时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
| 销售时段 销售数量 | 艾美特型号 | 格力型号 | 销售收入 |
| 第一周 | 5台 | 4台 | 2090元 |
| 第二周 | 4台 | 8台 | 2680元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某种货车自动卸货时的示意图,AC是水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC的夹角为30°,举升杠杆OB与底盘AC的夹角为75°,已知O与A的距离为4米,试求货车卸货时举升杠杆OB的长($\sqrt{2}≈1.414$,精确到0.01米).
如图是某种货车自动卸货时的示意图,AC是水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC的夹角为30°,举升杠杆OB与底盘AC的夹角为75°,已知O与A的距离为4米,试求货车卸货时举升杠杆OB的长($\sqrt{2}≈1.414$,精确到0.01米).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
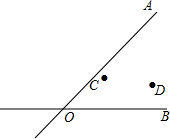 在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)
在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com