
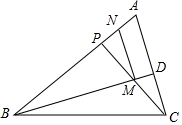
 如图,已知在△ABC中,P为边AB上一点,连接CP,M为CP的中点,连接BM并延长,交AC于点D,N为AP的中点,连接MN.若∠ACP=∠ABD.
如图,已知在△ABC中,P为边AB上一点,连接CP,M为CP的中点,连接BM并延长,交AC于点D,N为AP的中点,连接MN.若∠ACP=∠ABD.分析 (1)先根据M为CP的中点,N为AP的中点,得到MN是△ACP的中位线,得出NM∥AC,∠A=∠BNM,再根据∠ACP=∠ABD,判定△ACP∽△NBM,即可得出结论;
(2)先根据小三角形中位线定理,得到MN=$\frac{1}{2}$AC=1,再设AN=x,则AP=2x,根据AC•MN=BN•AP,得出方程2×1=(3-x)×2x,求得x的值,即可得到AP的长.
解答 解:(1)∵M为CP的中点,N为AP的中点,
∴MN是△ACP的中位线,
∴NM∥AC,MN=$\frac{1}{2}$AC,
∴∠A=∠BNM,
又∵∠ACP=∠ABD,
∴△ACP∽△NBM,
∴$\frac{AC}{NB}$=$\frac{AP}{NM}$,
∴AC•MN=BN•AP;
(2)∵AC=2,
∴MN=$\frac{1}{2}$AC=1,
设AN=x,则AP=2x,
∵AC•MN=BN•AP,
∴2×1=(3-x)×2x,
解得x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$,
∴AP=3+$\sqrt{5}$(舍去),AP=3-$\sqrt{5}$,
∴AP的长3-$\sqrt{5}$.
点评 本题主要考查了相似三角形才判定与性质以及一元二次方程的运用,解决问题的关键是掌握:有两组角对应相等的两个三角形相似.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每户居民一个月用水量的范围 | 水费价格(范围:元/立方米) |
| 不超过20立方米 | a |
| 超过20立方米 | 不超过部分仍为a元,超过部分为b元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com