
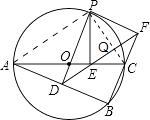
【题目】如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF. 
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是⊙O的切线.
【答案】
(1)解:∵AC=12,
∴CO=6,
∴ ![]() =
= ![]() =2π;
=2π;
答:劣弧PC的长为:2π
(2)证明:∵PE⊥AC,OD⊥AB,
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
 ,
,
∴△POE≌△AOD(AAS),
∴OD=EO
(3)证明:
法一:
如图,连接AP,PC,
∵OA=OP,
∴∠OAP=∠OPA,
由(2)得OD=EO,
∴∠ODE=∠OED,
又∵∠AOP=∠EOD,
∴∠OPA=∠ODE,
∴AP∥DF,
∵AC是直径,
∴∠APC=90°,
∴∠PQE=90°
∴PC⊥EF,
又∵DP∥BF,
∴∠ODE=∠EFC,
∵∠OED=∠CEF,
∴∠CEF=∠EFC,
∴CE=CF,
∴PC为EF的中垂线,
∴∠EPQ=∠QPF,
∵△CEP∽△CAP
∴∠EPQ=∠EAP,
∴∠QPF=∠EAP,
∴∠QPF=∠OPA,
∵∠OPA+∠OPC=90°,
∴∠QPF+∠OPC=90°,
∴OP⊥PF,
∴PF是⊙O的切线.
法二:
设⊙O的半径为r.
∵OD⊥AB,∠ABC=90°,
∴OD∥BF,∴△ODE∽△CFE
又∵OD=OE,∴FC=EC=r﹣OE=r﹣OD=r﹣ ![]() BC
BC
∴BF=BC+FC=r+ ![]() BC
BC
∵PD=r+OD=r+ ![]() BC
BC
∴PD=BF
又∵PD∥BF,且∠DBF=90°,
∴四边形DBFP是矩形
∴∠OPF=90°
OP⊥PF,
∴PF是⊙O的切线.

【解析】(1)根据弧长计算公式l= ![]() 进行计算即可;(2)证明△POE≌△ADO可得DO=EO;(3)连接AP,PC,证出PC为EF的中垂线,再利用△CEP∽△CAP找出角的关系求解.
进行计算即可;(2)证明△POE≌△ADO可得DO=EO;(3)连接AP,PC,证出PC为EF的中垂线,再利用△CEP∽△CAP找出角的关系求解.
【考点精析】利用切线的判定定理和弧长计算公式对题目进行判断即可得到答案,需要熟知切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0). 
(1)求此二次函数的解析式;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点. 
(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2ADNF=DEDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).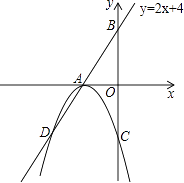
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 
A.函数有最小值
B.对称轴是直线x= ![]()
C.当x< ![]() ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).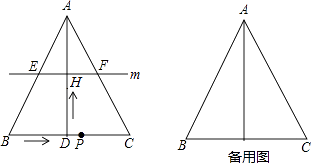
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市校计划购买甲、乙两种树苗共200株来绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲乙两种树苗成活率分别是90%和95%.
(1)若购买这种树苗共用去5600元,则甲、乙两种树苗各购买了多少株?
(2)如果要求这200株树苗的成活率不低于93%,那么乙种树苗至少要购买多少株.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com