
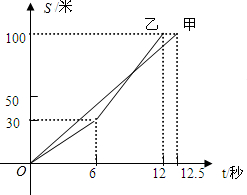
 甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:
甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:分析 (1)根据图象得出3.8秒时甲处于领先位置;
(2)根据图象得出乙先到达终点,且早到0.5秒,列出两个解析式得出两直线的交点解答;
(3)利用待定系数法得出甲的解析式即可.
解答 解:(1)由图象可得3.8秒时,甲处于领先位置;
(2)由图象可得:乙先到达终点,
且乙比甲早到12.5-12=0.5秒;
设甲的解析式为y=ax,
把(12.5,100)代入y=ax中,可得:100=12.5a,
解得:a=8,
所以甲的解析式为y=8x,
设乙的解析式为y=kx+b,
把(6,30)和(12,100)代入解析式y=kx+b,
可得:$\left\{\begin{array}{l}{6k+b=30}\\{12k+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{35}{3}}\\{b=-40}\end{array}\right.$.
所以解析式为:y=$\frac{35}{3}$x-40,
联立两个方程得:$\frac{35}{3}$x-40=8x,
解得:x=$\frac{120}{11}$.
所以$\frac{120}{11}$秒后甲同学被乙同学追上;
(3)设甲的解析式为S=at,
把(12.5,100)代入S=at中,可得:100=12.5a,
解得:a=8.
所以甲的解析式为S=8t.
点评 本题考查了函数的图象,还考查了学生从图象中读取信息的数形结合能力.解决此类识图题,同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
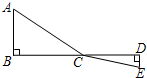 如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,DE⊥BD,连结AC,CE.
如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,DE⊥BD,连结AC,CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 化简:
化简:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com