
如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:⑴BP=CM;⑵△ABQ≌△CAP;⑶∠CMQ的度数始终等于60°;⑷当第 秒或第
秒或第 秒时,△PBQ为直角三角形.其中正确的结论有( )
秒时,△PBQ为直角三角形.其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
A.
【解析】
试题分析:A、在等边△ABC中,AB=BC.
∵点P、Q的速度都为1cm/s,
∴AP=PQ,
∴BP=CQ.
只有当CM=CQ时,BP=CM.故本选项错误;
B、∵△ABC是等边三角形
∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
∵ ,
,
∴△ABQ≌△CAP(SAS).
故本选项正确;
C、点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,
∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°.故本选项正确;
D、设时间为t秒,则AP=BQ=tcm,PB=(4-t)cm,
当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,即4-t=2t,t=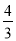 ,
,
当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(4-t),t=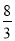 ,
,
∴当第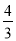 秒或第
秒或第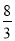 秒时,△PBQ为直角三角形.故本选项正确.
秒时,△PBQ为直角三角形.故本选项正确.
故选A.
考点:1.全等三角形的判定与性质;2.等边三角形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:解答题
八年级数学课上,曹老师出示了如下框中的题目.(本题8分)

小聪与同桌小明讨论后,进行了如下解答:
(1)特殊情况·探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=” ).

(2)特例启发·解答题目
【解析】
题目中, AE与DB的大小关系是:AE_____DB(填“>”,“<”或“=” ).
理由如下:如图2,过点E作EF∥BC,交AC于点F,
(请你完成以下解答过程)
(3)拓展结论·设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.
若△ABC的边长为2,AE=4,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.求证:△ABC≌△DEF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
若直角三角形斜边上的高和中线长分别是3cm,4 cm,则它的面积是 cm2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y= (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.

(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,DC是⊙O的直径,弦AB⊥CD于F,连结BC、DB,则下列结论错误的是( )

A. B.AF=BF C.OF=CF D.∠DBC=90º
B.AF=BF C.OF=CF D.∠DBC=90º
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题6分)已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以点C为圆心.AC为半径作⊙C,交AB于点D,求 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com