
����ѧ��ѧϰ�����У����Ǿ��������µ�̽�����̽��������⣮
��ѧ���⣺��������3�����㣬����������ڲ��ٻ�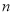 ���㣬������
���㣬������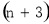 ����Ϊ���㻭�����Σ���ô���Լ��ö��ٸ������������Σ�
����Ϊ���㻭�����Σ���ô���Լ��ö��ٸ������������Σ�
̽�����ɣ�Ϊ�˽��������⣬���ǿ��Դ� ��
��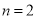 ��
�� �Ⱦ���ġ����������֣�̽�������Լ��õ������θ����ı仯���ɣ�
�Ⱦ���ġ����������֣�̽�������Լ��õ������θ����ı仯���ɣ�
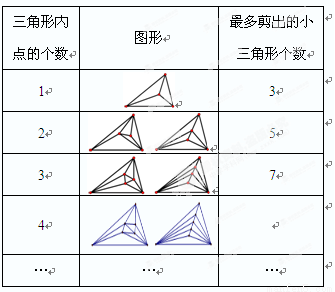
��1�������������������4����ʱ���ѱ���������
��2���㷢�ֵı仯�����ǣ� ��
��3�����룺���������ڵ�ĸ���Ϊ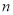 ʱ�������Լ��� �������Σ�
ʱ�������Լ��� �������Σ�
������ͨ���Լ����εĹ۲졢�����������һ���̽����������Ĺ��ɡ���������˼�뷽����Ϊ���ɣ�
�����������㳢���ù��ɵķ���̽����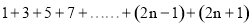 ���Ƕ��٣�
���Ƕ��٣�
 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ�����������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
һ�����������ϱ�ʾ�ĵ��ԭ��4����λ���ȣ�����ԭ�����ߣ���������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����н������۷�Ƭ���꼶��ѧ��12���¿���ѧ�Ծ��������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4����1���������߽�y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A������Ϊ��0��3����

��1����������ߵĽ���ʽ
��2������B���߶�AB�Ĵ��߽��������ڵ�D������Ե�CΪԲ�ĵ�Բ��ֱ��BD���У����ж������ߵĶԳ������C��������λ�ù�ϵ��������֤����
��3����֪��P���������ϵ�һ�����㣬��λ��A��C����֮�䣬�ʣ�����P�˶���ʲôλ��ʱ����PAC�������������ʱP�������͡�PAC����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����н������۷�Ƭ���꼶��ѧ��12���¿���ѧ�Ծ��������棩 ���ͣ������
��֪���� ��һԪ���η���
��һԪ���η��� ��ʵ��������
��ʵ�������� ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����н������۷�Ƭ���꼶��ѧ��12���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
�����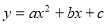 ��
�� ������
Ϊ������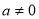 ���е�
���е� ��
��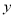 �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�����˽��ۣ�
��1�����κ��� ����Сֵ����СֵΪ
����Сֵ����СֵΪ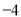 ��
��
��2����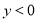 ����
����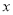 ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ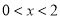 ��
��
��3�����κ��� ��ͼ����
��ͼ����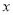 �����������㣬�����Ƿֱ���
�����������㣬�����Ƿֱ���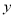 �����࣮
�����࣮
��������ȷ���۵ĸ����� �� ��
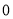 B��
B��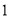 C��
C��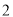 D��
D��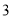
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���������꼶��12���¿���ѧ�Ծ��������棩 ���ͣ������
�Ȼ�������ֵ��5��3a2b��ab2����3��ab2+5a2b��������a= ��b=��
��b=�� ����8�֣�
����8�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���������꼶��12���¿���ѧ�Ծ��������棩 ���ͣ������
��a2��3b=5����6b��2a2+2015= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���������꼶��12���¿���ѧ�Ծ��������棩 ���ͣ������
��ͼ���ӳ��߶�AB��C��ʹBC=3AB����D���߶�BC���е㣬���CD=3cm����ô�߶�AC�ij����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ�����а��꼶��12���¿���ѧ�Ծ��������棩 ���ͣ������
����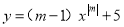 ��y����x��һ�κ�������m=______��
��y����x��һ�κ�������m=______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com