
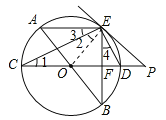
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)如图,连接OE,证明OE⊥PE即可得出PE是⊙O的切线;
(2)由圆周角定理得到∠AEB=∠CED=90°,进而得到∠3=∠4,结合已知条件证得结论;
(3)设EF=x,则CF=2x,在RT△OEF中,根据勾股定理求出EF的长,进而求得BE,CF的长,在RT△AEB中,根据勾股定理求出AE的长,然后根据△AEB∽△EFP,求出PF的长,即可求得PD的长.
试题解析:(1)如图,连接OE.∵CD是圆O的直径,∴∠CED=90°,∵OC=OE,∴∠1=∠2,又∵∠PED=∠C,即∠PED=∠1,∴∠PED=∠2,∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,∴OE⊥EP,又∵点E在圆上,∴PE是⊙O的切线;
(2)∵AB、CD为⊙O的直径,∴∠AEB=∠CED=90°,∴∠3=∠4(同角的余角相等),又∵∠PED=∠1,∴∠PED=∠4,即ED平分∠BEP;
(3)设EF=x,则CF=2x,∵⊙O的半径为5,∴OF=2x﹣5,在RT△OEF中, ![]() ,即
,即![]() ,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴
,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴![]() ,即
,即![]() ,∴PF=
,∴PF=![]() ,∴PD=PF﹣DF=
,∴PD=PF﹣DF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在创建全国森林城市的活动中,我区一“青年突击队”决定义务整修一条1000米长的绿化带,开工后,附近居民主动参加到义务劳动中,使整修的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时整修多少米长的绿化带?
查看答案和解析>>
科目:初中数学 来源: 题型:
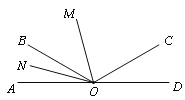
【题目】如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM、ON分别是∠AOC、∠AOB的平分线,∠MON=56°.
⑴ ∠COD与∠AOB相等吗?请说明理由;
⑵ 求∠BOC的度数;
⑶ 求∠AOB与∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差 | 0.023 | 0.018 | 0.020 | 0.021 |
则这10次跳绳中,这四个人发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
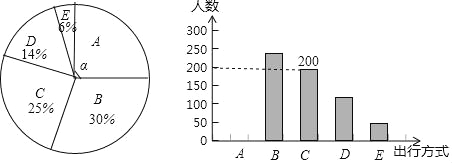
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com