
【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 .
【答案】
【解析】
试题分析:由点A(0,4),B(7,0),C(7,4),可得BC=OA=4,OB=AC=7,
分两种情况:
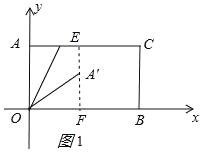
(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,如图1所示:
①当A'E:A'F=1:3时,
∵A'E+A'F=BC=4,
∴A'E=1,A'F=3,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() =
=![]() ,
,
∴A'(![]() ,3);
,3);
②当A'E:A'F=3:1时,同理得:A'(![]() ,1);
,1);
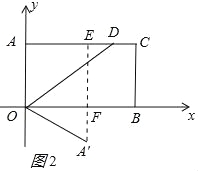
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,如图2所示:∵A'F:A'E=1:3,则A'F:EF=1:2,
∴A'F=![]() EF=
EF=![]() BC=2,
BC=2,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() =2
=2![]() ,
,
∴A'(2![]() ,﹣2);
,﹣2);
故答案为:(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).


科目:初中数学 来源: 题型:
【题目】小明在计算一个多项式加上5ab+4bc﹣3ac,不小心看成减去5ab+4bc﹣3ac,计算出结果为3ab﹣4bc+5ac,试求出原题目的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
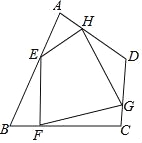
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班测量了10名学生的身高,他们的身高与对应的人数如下表所示
身高(cm) | 163 | 165 | 170 | 172 | 173 |
学生人数(人) | 1 | 2 | 3 | 2 | 2 |
则这10名学生身高的众数和中位数分别为( )
A.165cm,165cmB.170cm,165cm
C.165cm,170cmD.170cm,170cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com