
【题目】在创建全国森林城市的活动中,我区一“青年突击队”决定义务整修一条1000米长的绿化带,开工后,附近居民主动参加到义务劳动中,使整修的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时整修多少米长的绿化带?
科目:初中数学 来源: 题型:
【题目】已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(用含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.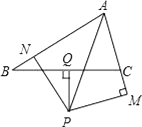
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦。我国西汉《周髀算经》中周公与商高对话中涉及勾股定理,所以这个定理也有人称商高定理,勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。
我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴,同时,增加一个垂直于x轴的数轴,叫做y轴,如下图。这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A。若平面上的点M ![]() ,N
,N ![]() ,我们定义点M、N在x轴方向上的距离为:
,我们定义点M、N在x轴方向上的距离为: ![]() ,点M、N在y轴方向上的距离为:
,点M、N在y轴方向上的距离为: ![]() 。例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5。
。例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5。
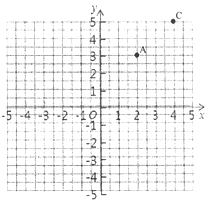
(1)若点B位置为(-1,-1),请在图中画出点B;图中点C的位置用数对______来表示。
(2)在(1)条件下,A、B两点在x轴方向上的距离为________,在y轴方向上的距离为_______,A、B两点间的距离为______;若E点、F点的位置分别为(a,b)、(c,d),点E、F之间的距离为|EF|,则![]() =_______________。
=_______________。
(3)有一个点D,它与(0,0)点的距离为1,请画出D点所有可能的位置。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……
请你参考上面的想法,帮助小宇证明∠APE =2∠MAD.(一种方法即可)
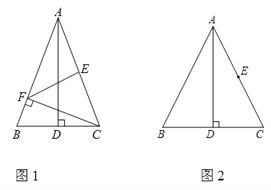
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com