
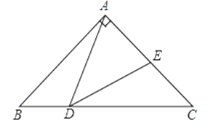
【题目】如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
【答案】(1)见解析;(2)1
【解析】
(1)首先根据等腰直角三角形的两个底角都是45![]() ,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
(2)根据等腰三角形的定义,此题要分AD=AE、AD=DE、AE=DE三种情况进行分析讨论.
(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2![]() ,AE=AC﹣EC=2﹣BD=2﹣(2
,AE=AC﹣EC=2﹣BD=2﹣(2![]() ﹣2)=4﹣2
﹣2)=4﹣2![]()
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE=![]() AC=1.
AC=1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图Rt![]() 中,∠A=30°,OB=2,如果将Rt
中,∠A=30°,OB=2,如果将Rt![]() 在坐标平面内,绕原点O按顺时针方向旋转到
在坐标平面内,绕原点O按顺时针方向旋转到![]() 的位置.
的位置.
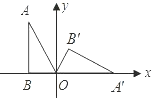
(1)求点![]() 的坐标.
的坐标.
(2)求顶点A从开始到![]() 点结束经过的路径长.
点结束经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
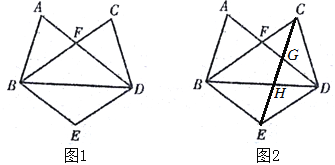
【题目】如图,AD与BC相交于点F,FA=FC,∠A=∠C,点E在BD的垂直平分线上.
(1)如图1,求证:∠FBE=∠FDE;
(2)如图2,连接CE分别交BD、AD于点H、G,当∠FBD=∠DBE=∠ABF,CD=DE时,直接写出所有与△ABF全等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第14个小房子用的石子数量为( )

A. 224B. 250C. 252D. 256
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com