
(本题满分12分)
知识迁移:
当 且
且 时,因为
时,因为 ≥
≥ ,所以
,所以 ≥
≥ ,从而
,从而 ≥
≥ (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为 .
.
直接应用:
已知函数 与函数
与函数 , 则当
, 则当 _________时,
_________时, 取得最小值为_________.变形应用:
取得最小值为_________.变形应用:
已知函数 与函数
与函数 ,求
,求 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的 的值.
的值.
实际应用:
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为 千米,求当
千米,求当 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
直接应用:1, 2 ;变形应用:当x=1时, 有最小值为4;实际应用:当x为600千米时,该汽车平均每千米的运输成本最低,最低是2.8元.
有最小值为4;实际应用:当x为600千米时,该汽车平均每千米的运输成本最低,最低是2.8元.
【解析】
试题分析:直接运用:可以直接套用套用所给的结论,即可得出结果.
变形运用:先得出 的表达式,然后将(x+1)看作一个整体,继而再运用所给结论即可.
的表达式,然后将(x+1)看作一个整体,继而再运用所给结论即可.
实际运用:设行驶x千米的费用为y,则可表示出平均每千米的运输成本,利用所给的距离即可得出答案.
试题解析:解:直接应用:因为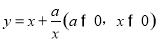 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值2
时,该函数有最小值2 ,所以函数
,所以函数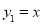
 与函数
与函数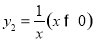 ,则当x=1时,
,则当x=1时,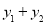 取得最小值为2.
取得最小值为2.
故答案为:1, 2 ;
变形应用:
解:∵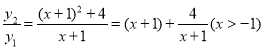 ,
,
∴ 有最小值为
有最小值为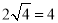 ,
,
当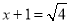 ,即
,即 时取得该最小值.
时取得该最小值.
实际应用:
解:设该汽车平均每千米的运输成本为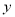 元,则
元,则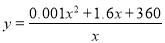
 ,
,
∴当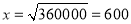 (千米)时, 该汽车平均每千米的运输成本
(千米)时, 该汽车平均每千米的运输成本 最低,最低成本为
最低,最低成本为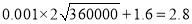 元.
元.
考点:二次函数的应用.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年安徽省七年级下学期开学考试数学试卷(解析版) 题型:解答题
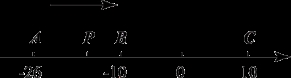
(9分)如图,已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从点A出发,以每秒1个单位的速度向终点C移动,当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,问当点Q从A点出发几秒钟时,点P和点Q相距2个单位长度? 直接写出此时点Q在数轴上表示的有理数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省八年级下学期开学考试数学试卷(解析版) 题型:选择题
如图,已知AB∥DE,∠ABC=80°,∠CDE=140°,则∠C=( )

A.20° B.30° C.40° D.50°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
若关于 的一元二次方程的两个根为
的一元二次方程的两个根为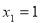 ,
,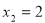 ,则这个方程是( )
,则这个方程是( )
A.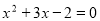 B.
B.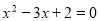
C.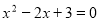 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分8分)班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如图1的频数分布折线图.
(1)请根据图1,回答下列问题:
①这个班共有______名学生,发言次数是5次的男生有____人、女生有____人;
②男、女生发言次数的中位数分别是____ 次和______次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2.求第二天发言次数增加3次的学生人数和全班增加的发言总次数.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
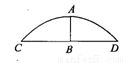
如图,有一圆弧形门拱的拱高AB为1m,跨度CD为4m,则这个圆弧形门拱的半径为 m.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题满分10分)某校学生参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:
销售单价x(单位:元/个) | 10 | 12 | 14 | 16 |
销售量y(单位:个) | 300 | 240 | 180 | 120 |
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com