
(本题满分8分)班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如图1的频数分布折线图.
(1)请根据图1,回答下列问题:
①这个班共有______名学生,发言次数是5次的男生有____人、女生有____人;
②男、女生发言次数的中位数分别是____ 次和______次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2.求第二天发言次数增加3次的学生人数和全班增加的发言总次数.

(1)①40;2;5;②4;5;(2)4人;52次.
【解析】
试题分析:(1)①男、女生人数相加即可的全班人数,在折线统计图中分别找到发言次数是5次的男生、女生人数;
②中位数是一组数据重新排序后之间的一个数或之间两个数的平均数,因此即可求解男、女生发言次数的中位数;
(2)先求出发言次数增加3次的学生人数的百分比,乘以全班人数,可得第二天发言次数增加3次的学生人数;分别求出发言次数增加的次数,相加即可.
试题解析:解:(1)①(2+1+6+4+2+3+2)+(1+2+3+2+5+4+3)=20+20=40名;
发言次数是5次的男生有2人,女生有5人;
故答案为:40;2;5;
②因为按从小到大排序后,男生第10个,11个都是4;女生第10个,11个都是5,
所以男、女生发言次数的中位数分别是4;5;
故答案为:4;5;
(2)发言次数增加3次的学生人数为:40×(1-20%-30%-40%)=4(人),
全班增加的发言总次数为:40%×40×1+30%×40×2+4×3=16+24+12=52(次).
考点:扇形统计图;折线统计图;中位数.
考点分析: 考点1:统计 统计学是在统计实践的基础上,自17世纪中叶产生并逐步发展起来的一门社会学科。它是研究如何测定、收集、整理、归纳和分析反映客观现象总体数量的数据,以便给出正确认识的方法论科学,被广泛的应用在各门学科之上,从自然科学和社会科学到人文科学,甚至被用来工商业及政府的情报决策之上。 试题属性

科目:初中数学 来源:2014-2015学年安徽省七年级下学期开学考试数学试卷(解析版) 题型:填空题
已知数列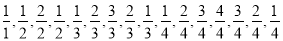 …,记第一个数
…,记第一个数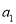 ,第二个数为
,第二个数为 ,…,第n个数为
,…,第n个数为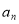 ,若
,若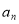 是方程
是方程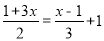 的解,则n =___________.
的解,则n =___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在 中,
中, ,
, 是
是 边上一点,以
边上一点,以 为直径的
为直径的 与边
与边 相切于点
相切于点 ,连结
,连结 并延长,与
并延长,与 的延长线交于点
的延长线交于点 .
.

(1)求证: ;
;
(2)若 ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
下列四个命题中,假命题是( )
A.两条对角线互相垂直且相等的四边形是正方形
B.菱形的一条对角线平分一组对角
C.顺次连结四边形的各边中点所得的四边形是平行四边形
D.对角线互相平分且相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分12分)
知识迁移:
当 且
且 时,因为
时,因为 ≥
≥ ,所以
,所以 ≥
≥ ,从而
,从而 ≥
≥ (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为 .
.
直接应用:
已知函数 与函数
与函数 , 则当
, 则当 _________时,
_________时, 取得最小值为_________.变形应用:
取得最小值为_________.变形应用:
已知函数 与函数
与函数 ,求
,求 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的 的值.
的值.
实际应用:
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为 千米,求当
千米,求当 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
已知α是锐角且tan α= ,则sin α+cos α= .
,则sin α+cos α= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如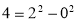 ,
,  ,
,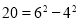 ,因此4,12,20都是“神秘数”
,因此4,12,20都是“神秘数”
(1)28和2012这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com