
(9分)如图,已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从点A出发,以每秒1个单位的速度向终点C移动,当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,问当点Q从A点出发几秒钟时,点P和点Q相距2个单位长度? 直接写出此时点Q在数轴上表示的有理数.
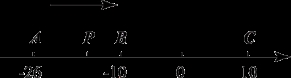
7秒或9秒;-5和1.
【解析】
试题分析:本题需要分两种情况进行讨论,①点Q追上点P之前,点P运动的路程-点Q运动的路程=2;②点Q追上点P之后,点Q运动的路程-点P匀速的路程=2.
试题解析:有两种情况:
(1)点Q追上点P之前相距2个单位长度.
设此时点Q从A点出发t秒钟.依题意,得 (16+t)-3t 解得,t=7.
此时点Q在数轴上表示的有理数为-5.
(2)点Q追上点P之后相距2个单位长度.
设此时点Q从A点出发m秒钟.依题意,得3m-(16+m)=2
解得,m =9.此时点Q在数轴上表示的有理数为1.
综上所述,当点Q从A点出发7秒和9秒时,点P和点Q相距2个单位长度,此时点Q在数轴上表示的有理数分别为-5和1.
考点:动点问题.
考点分析: 考点1:一元一次方程 定义:在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的整式方程叫一元一次方程。

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源:2014-2015学年山西农业大学附属中学八年级上学期期末考试数学试卷(解析版) 题型:填空题
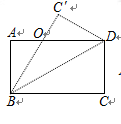
如图所示,△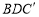 是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对。
是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:选择题
如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是( )

A.冷 B.静 C.应 D.考
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省八年级上学期期末考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,已知点P的坐标是(1,2),则点P关于y轴对称的点的坐标是( )
A.(1,2) B.(1, 2) C.(
2) C.( 1,2) D.(2,1)
1,2) D.(2,1)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省七年级下学期开学考试数学试卷(解析版) 题型:填空题
已知数列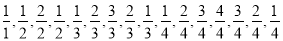 …,记第一个数
…,记第一个数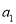 ,第二个数为
,第二个数为 ,…,第n个数为
,…,第n个数为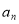 ,若
,若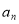 是方程
是方程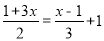 的解,则n =___________.
的解,则n =___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省七年级下学期开学考试数学试卷(解析版) 题型:选择题
如果y=3x,z=2(y-1),那么x-y+z等于( )
A.4x-1 B.4x-2 C.5x-1 D.5x-2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分12分)
知识迁移:
当 且
且 时,因为
时,因为 ≥
≥ ,所以
,所以 ≥
≥ ,从而
,从而 ≥
≥ (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为 .
.
直接应用:
已知函数 与函数
与函数 , 则当
, 则当 _________时,
_________时, 取得最小值为_________.变形应用:
取得最小值为_________.变形应用:
已知函数 与函数
与函数 ,求
,求 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的 的值.
的值.
实际应用:
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为 千米,求当
千米,求当 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com