
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_____________.

科目:初中数学 来源: 题型:
【题目】某学生由于看错了运算符号,把一个整式A减去多项式ab-2bc+3ac误认为加上这个多项式,结果得出的答案是2bc-3ac+2ab.
(1)求整式A;
(2)求原题的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)直接写出图1中所有的等腰三角形,并指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=10,AC=15,求△AEF的周长.
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由;若不存在,写出三者新的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC//OA,∠C=∠OAB=100°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值(提示:图中∠OFC=∠BOF+∠OBC);
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数;若不存在,说明理由(提示:三角形三个内角的和为180).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若单项式﹣xa+1y2与5ybx2是同类项,那么a、b的值分别是( )
A.a=1,b=1B.a=1,b=2C.a=1,b=3D.a=2,b=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国人很早就开始使用负数,中国古代数学著作《九章算术》.如果收入120元记作+120元,那么-100元表示( )
A.支出20元B.支出100元C.收入20元D.收入100元
查看答案和解析>>
科目:初中数学 来源: 题型:
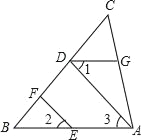
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com