Question

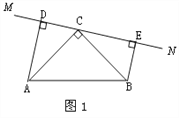
【题目】已知，如图1：△ABC中，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．

（1）直接写出图1中所有的等腰三角形，并指出EF与BE、CF间有怎样的数量关系？

（2）在（1）的条件下，若AB=10，AC=15，求△AEF的周长．

（3）如图2，若△ABC中，∠B的平分线与三角形外角∠ACG的平分线CO交于点O，过O点作OE∥BC交AB于E，交AC于F，请问（1）中EF与BE、CF间的关系还是否存在，若存在，说明理由；若不存在，写出三者新的数量关系，并说明理由．

Answer 1

【答案】（1）等腰△OBE和等腰△OCF；EF=BE+CF；（2）25；（3）（1）中EF与BE、CF间的关系不存在，新的数量关系为：EF=BE－CF

【解析】试题分析:(1)根据角平分线的性质可得: ∠ABO=∠CBO, ∠ACO=∠BCO,根据平行线的性质可得: ∠EOB=∠CBO, ∠FOC=∠BCO,即可求证: ∠ABO=∠EOB, ∠ACO=∠FOC,可求证:EO=EB,FO=FC,即EF=EO+FO=BE+CF,(2)根据(1)中的结论可得: △AEF的周长等于AE+AF+EF=AB+AC=10+15=25,(3) 根据角平分线的性质可得: ∠ABO=∠CBO, ∠ACO=∠BCO,根据平行线的性质可得: ∠EOB=∠CBO, ∠FOC=∠BCO,即可求证: ∠ABO=∠EOB, ∠ACO=∠FOC,可求证:EO=EB,FO=FC, 即EF=EO－FO=BE－CF．

试题解析:（1）有2个等腰三角形分别是:等腰△OBE和等腰△OCF,

EF=BE+CF．

（2）△AEF的周长为AE+AF+EF=AE+AF+OE+OF=AE+AF+BE+CF=AB+AC=25,

（3）（1）中EF与BE,CF间的关系不存在,新的数量关系为:EF=BE－CF,

证明:由BO平分∠ABC及OE∥BC可证BE=EO,

由CO平分∠ACG及OE∥BC可证CF=FO,

而EO=EF+OF,则EF=EO－OF=BE－CF .