
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
【答案】(1)![]() ,(-1,4); (2)
,(-1,4); (2)![]() ;(3) 平移距离为
;(3) 平移距离为![]() 或
或![]()
【解析】
(1)利用待定系数法构建方程组即可解决问题.
(2)利用勾股定理求出AD,CD,AC,证明∠ACD=90°即可解决问题.
(3)过点P作x轴的垂线,垂足为H.设P(a,-a2-2a+3),可得PH=|-a2-2a+3|,AH=a+3,由∠PAB=∠DAC,推出tan∠PAB=tan∠DAC=![]() .接下来分两种情形,构建方程求解即可.
.接下来分两种情形,构建方程求解即可.
解:(1)抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
根据题意,得:![]()
解得![]() ,
,![]() .
.
∴抛物线的表达式是![]() ,顶点
,顶点![]() 的坐标为(-1,4);
的坐标为(-1,4);
(2)∵A(-3,0),C(0,3),D(-1,4),
∴![]() ,
,
![]() ,
,
![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)过点![]() 作
作![]() 轴垂线,垂足为点
轴垂线,垂足为点![]() ,
,
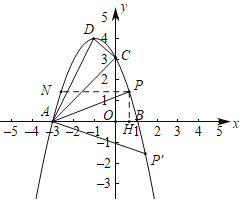
∵点![]() 是抛物线
是抛物线![]() 上一点,
上一点,
∴设![]() ,可得
,可得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ;
;
(ⅰ)![]() , 解得
, 解得![]() (舍去),
(舍去),![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
过点![]() 作
作![]() 轴平行线与抛物线
轴平行线与抛物线![]() 交于点
交于点![]() ,则点
,则点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
由抛物线的对称性可得![]() ,
,
∴平移距离为![]() ;
;
(ⅱ)![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
过点![]() 作
作![]() 轴平行线与抛物线
轴平行线与抛物线![]() 交于点
交于点![]() ,则点
,则点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
由抛物线的对称性可得![]() ,
,
∴平移距离为![]() ,
,
综上所述,平移距离为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B(t+4,0),线段AB的中点为C,若平面内存在一点P使得∠APC或者∠BPC为直角(点P不与A,B,C重合),则称P为线段AB的直角点.
(1)当t=0时,
①在点P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,线段AB的直角点是 ;
)中,线段AB的直角点是 ;
②直线y=![]() x+b上存在四个线段AB的直角点,直接写出b取值范围;
x+b上存在四个线段AB的直角点,直接写出b取值范围;
(2)直线y=![]() x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
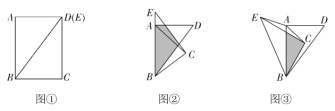
【题目】我们定义:将一个图形绕某一定点按某一方向旋转一定的角度(旋转角度小于等于360°),并且各边长伸缩相同的倍数得到另一个图形,如图①,这种变换叫做旋转伸缩变换,其中定点叫做旋转中心,对应边的比叫做伸缩比.
(特例感知)
(1)如图①,![]() 是等边三角形,
是等边三角形,![]() 绕点A作旋转伸缩变换得
绕点A作旋转伸缩变换得![]() ,连接
,连接![]() ,
,
①若![]() ,则旋转角的度数为________;
,则旋转角的度数为________;
②若伸缩比为2∶1,则线段![]() 的数量关系为________;
的数量关系为________;
③直线![]() 与直线
与直线![]() 所夹的锐角为________;
所夹的锐角为________;
(探究证明)
(2)如图②,在![]() 中,
中,![]() ,将
,将![]() 绕点A逆时针方向旋转一定的角度,作旋转伸缩变换得到
绕点A逆时针方向旋转一定的角度,作旋转伸缩变换得到![]() ,连接
,连接![]() 、
、![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点P,请判断
相交于点P,请判断![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(问题解决)
(3)在(2)的条件下,若![]() ,求当点
,求当点![]() 与点P重合时,
与点P重合时,![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老板经营甲、乙两个服装店铺,每个店铺各在同一段时间内都能售出A、B两种款式的服装合计30件且甲店售1件A款和2件B款可获得110元,售2件A和1件B可获得100元,乙店每售出一件A款获得27元,1件B款获利36元,
(1)问在甲店售出1件A和1件B分别获利多少元?
(2)某日王老板进了A款式的服装35件,B款式的服装25件,如果分配给甲店的A款式的服装x件,①求王老板获取的利润y(元)与x(件)之间的函数关系式,并写出x的取值范围;
②由于甲、乙两个店铺所处的地段原因,王老板想在保证乙店利润不小于950元的前提下,使得自己获取的利润最大,请你帮王老板设计一种最佳分配方案,并求最大的总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题与情境)
在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图①,现有矩形纸片![]() .连接
.连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 位置不变,将
位置不变,将![]() 从图①的位置开始,绕点B按逆时针方向旋转,旋转角为
从图①的位置开始,绕点B按逆时针方向旋转,旋转角为![]() .
.
(操作发现)
(1)在![]() 旋转过程中,连接
旋转过程中,连接![]() ,则当
,则当![]() 时,
时,![]() 的值是________;
的值是________;
(2)如图②,将图①中的![]() 旋转,当点E落在
旋转,当点E落在![]() 延长线上时停止旋转,求出此时
延长线上时停止旋转,求出此时![]() 的值;
的值;
(实践探究)
(3)如图③,将图②中的![]() 继续旋转,当
继续旋转,当![]() 时停止旋转,直接写出此时
时停止旋转,直接写出此时![]() 的度数,并求出
的度数,并求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
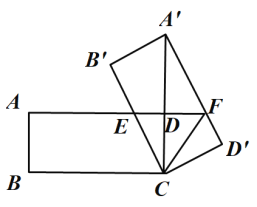
【题目】如图,在矩形ABCD中, AB=3,BC=4,将矩形ABCD绕点C旋转,点A、B、D的对应点分别为A’ 、B’、 D’,当A’ 落在边CD的延长线上时,边A’ D’ 与边 AD的延长线交于点F,联结CF,那么线段CF的长度为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
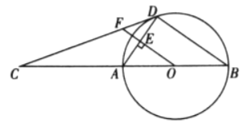
【题目】如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)求证:∠ADC=∠AOF;
(2)若sinC=![]() ,BD=8,求EF的长.
,BD=8,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某校初二年级的同学乘坐大巴车去北京展览馆参观“砥砺奋进的五年”大型成就展,北京展览馆距离该校12千米,1号车出发3分钟后,2号车才出发,结果两车同时到达,已知2号车的平均速度是1号车的平均速度的1.2倍,求2号车的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分B.相等C.互相垂直D.互相垂直平分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com