
【题目】王老板经营甲、乙两个服装店铺,每个店铺各在同一段时间内都能售出A、B两种款式的服装合计30件且甲店售1件A款和2件B款可获得110元,售2件A和1件B可获得100元,乙店每售出一件A款获得27元,1件B款获利36元,
(1)问在甲店售出1件A和1件B分别获利多少元?
(2)某日王老板进了A款式的服装35件,B款式的服装25件,如果分配给甲店的A款式的服装x件,①求王老板获取的利润y(元)与x(件)之间的函数关系式,并写出x的取值范围;
②由于甲、乙两个店铺所处的地段原因,王老板想在保证乙店利润不小于950元的前提下,使得自己获取的利润最大,请你帮王老板设计一种最佳分配方案,并求最大的总利润是多少?
【答案】(1)在甲店售出1件A和1件B分别获利30元、40元;(2)①![]() ;②最佳分配方案是在甲店出售A种款式的服装21件,B种款式的服装9件,在乙服装店出售A种款式的服装14件,出售B种款式的服装16件,最大的总利润是1944元
;②最佳分配方案是在甲店出售A种款式的服装21件,B种款式的服装9件,在乙服装店出售A种款式的服装14件,出售B种款式的服装16件,最大的总利润是1944元
【解析】
解:(1)设在甲店售出1件A和1件B分别获利a元、b元,
![]() ,得
,得![]() ,
,
答:在甲店售出1件A和1件B分别获利30元、40元;
(2)①由题意可得,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即王老板获取的利润y(元)与x(件)之间的函数关系式是![]() ;
;
②![]() 王老板想在保证乙店利润不小于950元,
王老板想在保证乙店利润不小于950元,
![]() ,
,
解得,![]() ,
,
![]() ,
,
![]() 当
当![]() 时,y取得最大值,此时
时,y取得最大值,此时![]() ,
,![]() ,
,![]() ,
,![]() ,
,
答:最佳分配方案是在甲店出售A种款式的服装21件,B种款式的服装9件,在乙服装店出售A种款式的服装14件,出售B种款式的服装16件,最大的总利润是1944元.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF=![]() ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
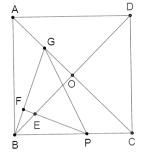
①![]() ;②PE=2BF;③在点P运动的过程中,当GB=GP时,
;②PE=2BF;③在点P运动的过程中,当GB=GP时,![]() ;④当P为BC的中点时,
;④当P为BC的中点时,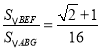 .
.
A.①②③B..①②④C.②③④D..①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大润发”、“世纪联华”两家超市出售同样的洗衣液和香皂,洗衣液和香皂在两家超市的售价分别一样.已知买1袋洗衣液和2块香皂要花费48元,买3袋洗衣液和4块香皂要花费134元.
(1)一袋洗衣液与一块香皂售价各是多少元?(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“大润发”超市规定:这两种商品都打八五折;“世纪联华”超市规定:买一袋洗衣液赠送一块香皂.若妈妈想要买4袋洗衣液和10块香皂,又只能在一家超市购买,你觉得选择哪家超市购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前夕,某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费125元,购进A品牌文具袋3个和B品牌文具袋各4个共花费90元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为y元.
①求y关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不超过进货价格的40%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
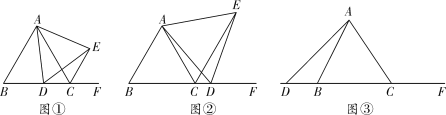
【题目】已知![]() 为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边
为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边![]() (顶点A、D、E按逆时针方向排列),连接CE.
(顶点A、D、E按逆时针方向排列),连接CE.
(1)问题发现
如图①,当点D在边BC上时,填空:
①线段BD,CE之间的数量关系为________;
②线段AC、CE、CD三者之间的数量关系为________;
(2)拓展研究
如图②,当点D在边BC的延长线上且其他条件不变时,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)解决问题
如图③,当点D在边BC的反向延长线上且其他条件不变时,若![]() ,
,![]() ,请直接写出线段CD的长.
,请直接写出线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
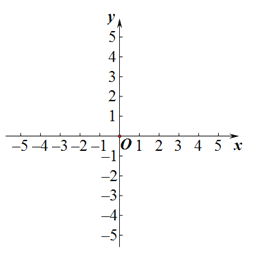
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦
中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦![]() (
(![]() 分别为点A,B的对应点),线段
分别为点A,B的对应点),线段![]() 长度的最小值称为线段AB到⊙O的“平移距离”.
长度的最小值称为线段AB到⊙O的“平移距离”.
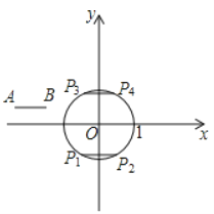
(1)如图,平移线段AB到⊙O的长度为1的弦![]() 和
和![]() ,则这两条弦的位置关系是 ;在点
,则这两条弦的位置关系是 ;在点![]() 中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线![]() 上,记线段AB到⊙O的“平移距离”为
上,记线段AB到⊙O的“平移距离”为![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点A的坐标为![]() ,记线段AB到⊙O的“平移距离”为
,记线段AB到⊙O的“平移距离”为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为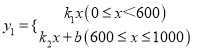 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).
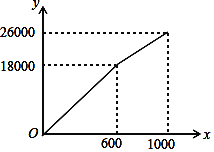
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com