
【题目】如图,![]() 是
是![]() 的直径,点D在
的直径,点D在![]() 上,
上,![]() 的延长线与过点B的切线交于点C,E为线段
的延长线与过点B的切线交于点C,E为线段![]() 上的点,过点E的弦
上的点,过点E的弦![]() 于点H.
于点H.

(1)求证:![]() ;
;
(2)已知![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() -2.
-2.
【解析】
(1)连接BD,根据圆周角定理得到∠ADB=90°,根据切线的性质得到∠ABC=90°,得到∠C=∠ABD,根据圆周角定理即可得到结论;
(2)根据相似三角形的判定和性质以及勾股定理即可得到结论.
解:(1)证明:如图1,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵BC是⊙O的切线,
∴∠ABC=90°,
∴∠C+∠CAB=90°,
∴∠C=∠ABD,
∵∠AGD=∠ABD,
∴∠AGD=∠C;
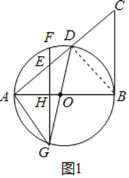
(2)解:∵∠BDC=∠ABC=90°,∠C=∠C,
∴△ABC∽△BDC,
∴![]() ,
,
∴![]() ,
,
∴AC=9,
∴AB=![]() ,
,
∵CE=2AE,
∴AE=3,CE=6,
∵FH⊥AB,
∴FH∥BC,
∴△AHE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AH=![]() ,EH=2,
,EH=2,
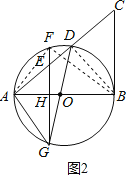
如图2,连接AF,BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠AFH+∠BFH=∠AFH+∠FAH=90°,
∴∠FAH=∠BFH,
∴△AFH∽△FBH,
∴![]() ,
,
∴![]() ,
,
∴FH=![]() ,
,
∴EF=![]() -2.
-2.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
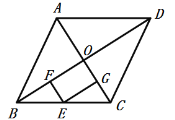
【题目】如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位食堂为全体名职工提供了![]() 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取
四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取![]() 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
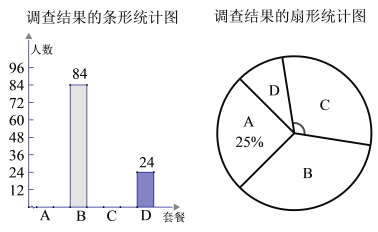
![]() 在抽取的
在抽取的![]() 人中最喜欢
人中最喜欢![]() 套餐的人数为 ,扇形统计图中“
套餐的人数为 ,扇形统计图中“![]() ”对应扇形的圆心角的大小为 ;
”对应扇形的圆心角的大小为 ;
![]() 依据本次调查的结果,估计全体
依据本次调查的结果,估计全体![]() 名职工中最喜欢
名职工中最喜欢![]() 套餐的人数;
套餐的人数;
![]() 现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教职工为庆祝“建国![]() 周年”开展学习强国知识竞赛,本次知识竞赛分为甲、乙、丙三组进行.下面两幅统计图反映了教师参加学习强国知识竞赛的报名情况,请你根据图中的信息回答下列问题:
周年”开展学习强国知识竞赛,本次知识竞赛分为甲、乙、丙三组进行.下面两幅统计图反映了教师参加学习强国知识竞赛的报名情况,请你根据图中的信息回答下列问题:
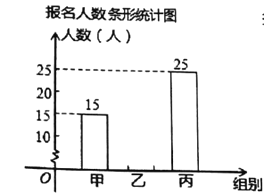
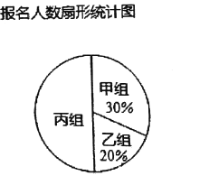
(1)该校教师报名参加本次学习强国知识竞赛的总人数为___________人,并补全条形统计图;
(2)该校教师报名参加丙组的人数所占圆心角度数是__________;
(3)根据实际情况,需从甲组抽调部分教师到丙组,使丙组人数是甲组人数的![]() 倍,应从甲组抽调多少名教师到丙组?
倍,应从甲组抽调多少名教师到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
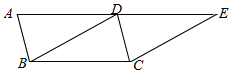
【题目】如图,四边形ABCD是平行四边形,AD=BD,过点C作CE∥BD,交AD的延长线于点E.
(1)求证:四边形BDEC是菱形;
(2)连接BE,若AB=2,AD=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B(t+4,0),线段AB的中点为C,若平面内存在一点P使得∠APC或者∠BPC为直角(点P不与A,B,C重合),则称P为线段AB的直角点.
(1)当t=0时,
①在点P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,线段AB的直角点是 ;
)中,线段AB的直角点是 ;
②直线y=![]() x+b上存在四个线段AB的直角点,直接写出b取值范围;
x+b上存在四个线段AB的直角点,直接写出b取值范围;
(2)直线y=![]() x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的半径为
的半径为![]() ,
,![]() 的半径为
的半径为![]() ,以
,以![]() 为圆心,以
为圆心,以![]() 的长为半径画弧,再以线段
的长为半径画弧,再以线段![]() 的中点P为圆心,以
的中点P为圆心,以![]() 的长为半径画弧,两弧交于点A,连接
的长为半径画弧,两弧交于点A,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点B,过点B作
于点B,过点B作![]() 的平行线
的平行线![]() 交
交![]() 于点C.
于点C.
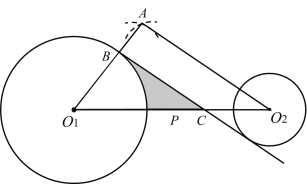
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老板经营甲、乙两个服装店铺,每个店铺各在同一段时间内都能售出A、B两种款式的服装合计30件且甲店售1件A款和2件B款可获得110元,售2件A和1件B可获得100元,乙店每售出一件A款获得27元,1件B款获利36元,
(1)问在甲店售出1件A和1件B分别获利多少元?
(2)某日王老板进了A款式的服装35件,B款式的服装25件,如果分配给甲店的A款式的服装x件,①求王老板获取的利润y(元)与x(件)之间的函数关系式,并写出x的取值范围;
②由于甲、乙两个店铺所处的地段原因,王老板想在保证乙店利润不小于950元的前提下,使得自己获取的利润最大,请你帮王老板设计一种最佳分配方案,并求最大的总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com