
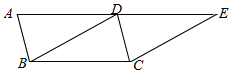
【题目】如图,四边形ABCD是平行四边形,AD=BD,过点C作CE∥BD,交AD的延长线于点E.
(1)求证:四边形BDEC是菱形;
(2)连接BE,若AB=2,AD=4,求BE的长.
【答案】(1)见解析 (2)![]()
【解析】
(1)由平行四边形的性质可得AD∥BC,AD=BC=BD,由两组对边平行的四边形是平行四边形,可证四边形BDEC是平行四边形,即可得结论;
(2)连接BE交CD于O,由菱形的性质可得DO=CO=![]() CD=1,BO=
CD=1,BO=![]() BE,CD⊥BE,由勾股定理可求BO的长,即可求解.
BE,CD⊥BE,由勾股定理可求BO的长,即可求解.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=CD,
∵AD=BD,
∴BD=BC,
∵CE∥BD,AD∥BC,
∴四边形BDEC是平行四边形,
又∵BD=BC,
∴四边形BDEC是菱形;
(2)如图,连接BE交CD于O,
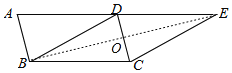
∵四边形BDEC是菱形,
∴DO=CO=![]() CD=1,BO=
CD=1,BO=![]() BE,CD⊥BE,
BE,CD⊥BE,
在Rt△BDO中,AD=BD=4,DO=1,
∴BO=![]() ,
,
∴BE=2BO=![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
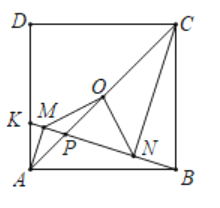
【题目】如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1)求证:AM=BN;
(2)请判断△OMN的形状,并说明理由;
(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为![]() ,请直接写出AK长.
,请直接写出AK长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的综合素养,某校开设了五门手工活动课.按照类别分为:![]() “剪纸”、
“剪纸”、![]() “沙画”、
“沙画”、![]() “葫芦雕刻”、
“葫芦雕刻”、![]() “泥塑”、
“泥塑”、![]() “插花”.为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如下两幅不完整的统计图.
“插花”.为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如下两幅不完整的统计图.
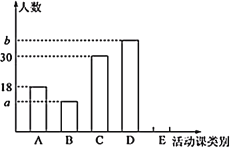
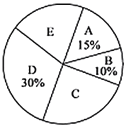
根据以上信息,回答下列问题:
(1)本次调查的样本容量为________;统计图中的![]() ________,
________,![]() ________;
________;
(2)通过计算补全条形统计图;
(3)该校共有2500名学生,请你估计全校喜爱“葫芦雕刻”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴的正半轴交于点A,与
轴的正半轴交于点A,与![]() 轴的负半轴交于点B,
轴的负半轴交于点B, ![]() ,过点A作
,过点A作![]() 轴的垂线与过点O的直线相交于点C,直线OC的解析式为
轴的垂线与过点O的直线相交于点C,直线OC的解析式为![]() ,过点C作
,过点C作![]() 轴,垂足为
轴,垂足为![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;
(2)如图2,点N在线段![]() 上,连接ON,点P在线段ON上,过P点作
上,连接ON,点P在线段ON上,过P点作![]() 轴,垂足为D,交OC于点E,若
轴,垂足为D,交OC于点E,若![]() ,求
,求![]() 的值;
的值;
(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作![]() 轴的平行线交BQ于点G,连接PF交
轴的平行线交BQ于点G,连接PF交![]() 轴于点H,连接EH,若
轴于点H,连接EH,若![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=ax2﹣2ax+c的图象经过点A(﹣1,1),将A点向右平移3个单位长度,再向上平移2个单位长度,得到点B,直线y=2x+m经过点B,与y轴交于点C.
(1)求点B,C的坐标;
(2)求二次函数图象的对称轴;
(3)若二次函数y=ax2﹣2ax+c(﹣1<x<2)的图象与射线CB恰有一个公共点,结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
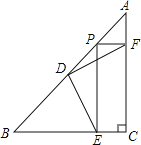
(1)探究DE与DF的关系,并给出证明;
(2)当点P满足什么条件时,线段EF的长最短?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线![]() ,点A、B分别在
,点A、B分别在![]() 、
、![]() 上,斜坡AB的长为18米,过点B作
上,斜坡AB的长为18米,过点B作![]() 于点C,且线段AC的长为
于点C,且线段AC的长为![]() 米.
米.
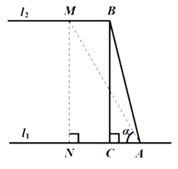
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚![]() 为60°,过点M作
为60°,过点M作![]() 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
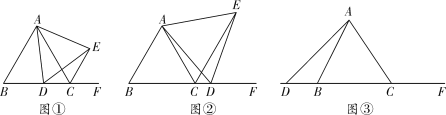
【题目】已知![]() 为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边
为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边![]() (顶点A、D、E按逆时针方向排列),连接CE.
(顶点A、D、E按逆时针方向排列),连接CE.
(1)问题发现
如图①,当点D在边BC上时,填空:
①线段BD,CE之间的数量关系为________;
②线段AC、CE、CD三者之间的数量关系为________;
(2)拓展研究
如图②,当点D在边BC的延长线上且其他条件不变时,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)解决问题
如图③,当点D在边BC的反向延长线上且其他条件不变时,若![]() ,
,![]() ,请直接写出线段CD的长.
,请直接写出线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com