
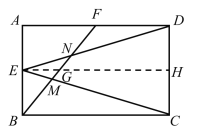
【题目】如图,在矩形![]() 中,
中,![]() 分别为边
分别为边![]() ,
,![]() 的中点,
的中点,![]() 与
与![]() ,
,![]() 分别交于点M,N.已知
分别交于点M,N.已知![]() ,
,![]() ,则
,则![]() 的长为_________.
的长为_________.

【答案】![]()
【解析】
过点E作EH∥AD,交点BF于点G,交CD于点H,证明△BEG∽△BAF,求出EG的长,再证明△EGN∽△DFN,△EGM∽△CBM,得出![]() ,
,![]() ,再求出BG=GF=
,再求出BG=GF=![]() BF=
BF=![]() ,从而求出NG和MG,可得MN的长.
,从而求出NG和MG,可得MN的长.
解:过点E作EH∥AD,交点BF于点G,交CD于点H,
由题意可知:EH∥BC,
∴△BEG∽△BAF,
∴![]() ,
,
∵AB=4,BC=6,点E为AB中点,F为AD中点,
∴BE=2,AF=3,
∴![]() ,
,
∴EG=![]() ,
,
∵EH∥BC,
∴△EGN∽△DFN,△EGM∽△CBM,
∴![]() ,
,![]() ,
,
∴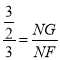 ,
,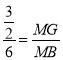 ,
,
即![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵E为AB中点,EH∥BC,
∴G为BF中点,
∴BG=GF=![]() BF=
BF=![]() ,
,
∴NG=![]() =
=![]() ,MG=
,MG=![]() BG=
BG=![]() ,
,
∴MN=NG+MG=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织了一次全校![]() 名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于
名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于![]() 分,为了更好的了解本次大赛的成绩分布情况,随机抽取了
分,为了更好的了解本次大赛的成绩分布情况,随机抽取了![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行整理,得到下列不完整的统计图表:
分)作为样本进行整理,得到下列不完整的统计图表:
成绩在这![]() 组的数据是:
组的数据是:
![]()
![]()
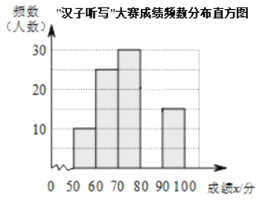
“汉字听写”大赛成绩段频数频率统计表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)表中![]() ,
,![]() ;
;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生获得优胜奖,估计该校参加这次比赛的
分)的学生获得优胜奖,估计该校参加这次比赛的![]() 名学生中获得优胜奖的人数.
名学生中获得优胜奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
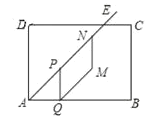
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交边
的角平分线交边![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上以每秒
上以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向从点
方向从点![]() 开始运动,过点
开始运动,过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边向右作平行四边形
为边向右作平行四边形![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() ,设
,设![]() 点运动时间为
点运动时间为![]() 秒.
秒.
(1)![]() ____________(用含
____________(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与矩形
与矩形![]() 重合部分面积为
重合部分面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)直接写出在点![]() 、
、![]() 运动的过程中,整个图形中形成的三角形存在全等三角形时
运动的过程中,整个图形中形成的三角形存在全等三角形时![]() 的值(不添加任何辅助线).
的值(不添加任何辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
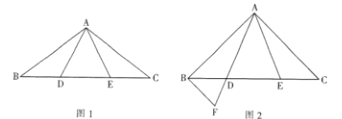
【题目】已知,在![]() 中,
中,![]() ,点D,点E在BC上,
,点D,点E在BC上,![]() ,连接
,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,过点B作
时,过点B作![]() ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)若cos∠PAB=![]() ,BC=2,求PO的长.
,BC=2,求PO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前夕,某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费125元,购进A品牌文具袋3个和B品牌文具袋各4个共花费90元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为y元.
①求y关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不超过进货价格的40%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com