
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)若cos∠PAB=![]() ,BC=2,求PO的长.
,BC=2,求PO的长.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】某公园的门票价格如表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b(a≥b).若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则共需支付门票费为990元,那么这两个部门的人数a=_____;b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B(t+4,0),线段AB的中点为C,若平面内存在一点P使得∠APC或者∠BPC为直角(点P不与A,B,C重合),则称P为线段AB的直角点.
(1)当t=0时,
①在点P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,线段AB的直角点是 ;
)中,线段AB的直角点是 ;
②直线y=![]() x+b上存在四个线段AB的直角点,直接写出b取值范围;
x+b上存在四个线段AB的直角点,直接写出b取值范围;
(2)直线y=![]() x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
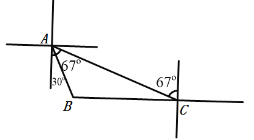
【题目】如图,观测站C发现在它的正西方向,有一艘渔船B出现险情,需救援,当即上报救援中心A,测得C在A的南偏东67方向,距A处50海里,而B在A的南偏东30方向,求渔船B与救援中心A的距离AB,渔船B与观测站C的距离BC.(结果精确到0.1海里)(参考数据:sin37=0.6,cos37=0.8,tan37=![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是![]() 的直径,点C是
的直径,点C是![]() 上一点,连接AC、BC,直线MN过点C,满足
上一点,连接AC、BC,直线MN过点C,满足![]() .
.
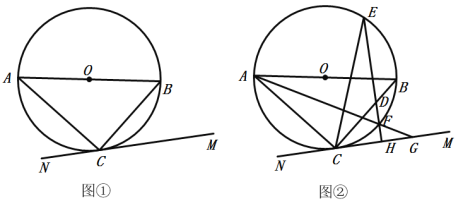
(1)如图①,求证:直线MN是![]() 的切线;
的切线;
(2)如图②,点D在线段BC上,过点D作![]() 于点H,直线DH交
于点H,直线DH交![]() 于点E、F,连接AF并延长交直线MN于点G,连接CE,且
于点E、F,连接AF并延长交直线MN于点G,连接CE,且![]() ,若
,若![]() 的半径为1,
的半径为1,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
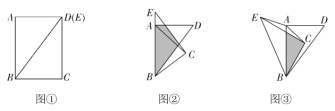
【题目】(问题与情境)
在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图①,现有矩形纸片![]() .连接
.连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 位置不变,将
位置不变,将![]() 从图①的位置开始,绕点B按逆时针方向旋转,旋转角为
从图①的位置开始,绕点B按逆时针方向旋转,旋转角为![]() .
.
(操作发现)
(1)在![]() 旋转过程中,连接
旋转过程中,连接![]() ,则当
,则当![]() 时,
时,![]() 的值是________;
的值是________;
(2)如图②,将图①中的![]() 旋转,当点E落在
旋转,当点E落在![]() 延长线上时停止旋转,求出此时
延长线上时停止旋转,求出此时![]() 的值;
的值;
(实践探究)
(3)如图③,将图②中的![]() 继续旋转,当
继续旋转,当![]() 时停止旋转,直接写出此时
时停止旋转,直接写出此时![]() 的度数,并求出
的度数,并求出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com