
【题目】如图,观测站C发现在它的正西方向,有一艘渔船B出现险情,需救援,当即上报救援中心A,测得C在A的南偏东67方向,距A处50海里,而B在A的南偏东30方向,求渔船B与救援中心A的距离AB,渔船B与观测站C的距离BC.(结果精确到0.1海里)(参考数据:sin37=0.6,cos37=0.8,tan37=![]() ,
,![]() ≈1.73)
≈1.73)
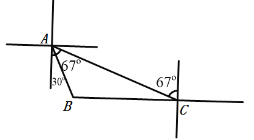
【答案】AB的长约为23.7海里,BC的长约为34.6海里
【解析】
过点C,作CD⊥AB,交AB的延长线于点D,构造Rt△ABC,求出AD、CD,根据三角函数值求出BC即可.
解:过点C,作CD⊥AB,交AB的延长线于点D,构造Rt△ABC,求出AD、CD,根据三角函数值求出BC即可.
在Rt△ABC中,
cos37![]() =
=![]() ,
,
∴AD=50×0.8=40,
CD=50×sin37=30 ,
∴在Rt△BCD中,
∵B在A的南偏东30方向,
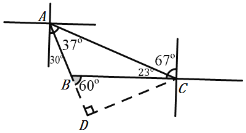
∴∠DBC= 60 ,
∴tan60=![]() ,
,
∴BD=10![]() ,
,
∴AB=40-![]() ,
,
≈40-10×1.73
=23.7.
又∵cos60=![]() ,
,
∴BC=20![]() ≈34.6,
≈34.6,
答:AB的长约为23.7海里,BC的长约为34.6海里.


科目:初中数学 来源: 题型:
【题目】在防疫工作稳步推进的过程中,复工复产工作也在如火如荼进行.某企业计划通过扩大生产能力来消化第一季度积累的订单,决定增加一条新的生产线并招收工人.根据以往经验,一名熟练工人每小时完成的工件数量比一名普通工人每小时完成的工件数量多10个,且一名熟练工人完成160个工件与一名普通工人完成80个工件所用的时间相同.
(1)求一名熟练工人和一名普通工人每小时分别能完成多少个工件;
(2)新生产线的目标产能是每小时生产200个工件,计划招聘![]() 名普通工人与
名普通工人与![]() 名熟练工人共同完成这项任务,请写出
名熟练工人共同完成这项任务,请写出![]() 与
与![]() 的函数关系式(不需要写自变量
的函数关系式(不需要写自变量![]() 的取值范围);
的取值范围);
(3)该企业在做市场调研时发现,一名普通工人每天工资为120元,一名熟练工人每天工资为150元,而且本地区现有熟练工人不超过8人.在(2)的条件下,该企业如何招聘工人,使得工人工资的总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点D,点E在BC上,
,点D,点E在BC上,![]() ,连接
,连接![]() .
.
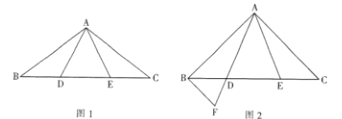
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,过点B作
时,过点B作![]() ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)若cos∠PAB=![]() ,BC=2,求PO的长.
,BC=2,求PO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
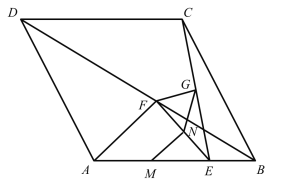
【题目】如图,菱形![]() 的边长为1,
的边长为1,![]() ,点E是边
,点E是边![]() 上任意一点(端点除外),线段
上任意一点(端点除外),线段![]() 的垂直平分线交
的垂直平分线交![]() ,
,![]() 分别于点F,G,
分别于点F,G,![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
(1)求证:![]() ;
;
(2)求![]() 的最小值;
的最小值;
(3)当点E在![]() 上运动时,
上运动时,![]() 的大小是否变化?为什么?
的大小是否变化?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .点P是平面内不与A,C重合的任意一点,连接
.点P是平面内不与A,C重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转
绕点P逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .点M是
.点M是![]() 的中点,点N是
的中点,点N是![]() 的中点.
的中点.
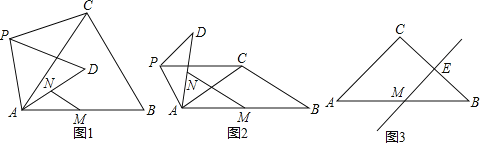
(1)问题发现
如图1,当![]() 时,
时,![]() 的值是________,直线
的值是________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究
如图2,当![]() 时,请写出的
时,请写出的![]() 值及直线
值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
如图3,当![]() 时,若点E是
时,若点E是![]() 的中点,点P在直线
的中点,点P在直线![]() 上,请直接写出点B,P,D在同一条直线上时
上,请直接写出点B,P,D在同一条直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4.D是边AB的中点,点E为边AC上的一个动点(与点A、C不重合),过点E作EF∥AB,交边BC于点F.联结DE、DF,设CE=x.

(1)当x =1时,求△DEF的面积;
(2)如果点D关于EF的对称点为D’,点D’ 恰好落在边AC上时,求x的值;
(3)以点A为圆心,AE长为半径的圆与以点F为圆心,EF长为半径的圆相交,另一个交点H恰好落在线段DE上,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com