
【题目】AB是![]() 的直径,点C是
的直径,点C是![]() 上一点,连接AC、BC,直线MN过点C,满足
上一点,连接AC、BC,直线MN过点C,满足![]() .
.
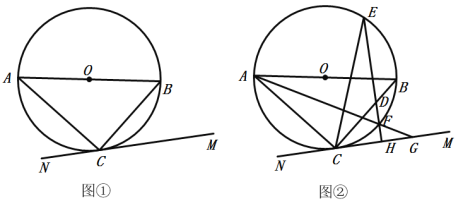
(1)如图①,求证:直线MN是![]() 的切线;
的切线;
(2)如图②,点D在线段BC上,过点D作![]() 于点H,直线DH交
于点H,直线DH交![]() 于点E、F,连接AF并延长交直线MN于点G,连接CE,且
于点E、F,连接AF并延长交直线MN于点G,连接CE,且![]() ,若
,若![]() 的半径为1,
的半径为1,![]() ,求
,求![]() 的值.
的值.
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交边
的角平分线交边![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上以每秒
上以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向从点
方向从点![]() 开始运动,过点
开始运动,过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边向右作平行四边形
为边向右作平行四边形![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() ,设
,设![]() 点运动时间为
点运动时间为![]() 秒.
秒.
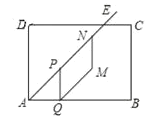
(1)![]() ____________(用含
____________(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与矩形
与矩形![]() 重合部分面积为
重合部分面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)直接写出在点![]() 、
、![]() 运动的过程中,整个图形中形成的三角形存在全等三角形时
运动的过程中,整个图形中形成的三角形存在全等三角形时![]() 的值(不添加任何辅助线).
的值(不添加任何辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)若cos∠PAB=![]() ,BC=2,求PO的长.
,BC=2,求PO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的边长为1,
的边长为1,![]() ,点E是边
,点E是边![]() 上任意一点(端点除外),线段
上任意一点(端点除外),线段![]() 的垂直平分线交
的垂直平分线交![]() ,
,![]() 分别于点F,G,
分别于点F,G,![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
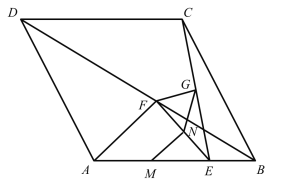
(1)求证:![]() ;
;
(2)求![]() 的最小值;
的最小值;
(3)当点E在![]() 上运动时,
上运动时,![]() 的大小是否变化?为什么?
的大小是否变化?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF=![]() ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
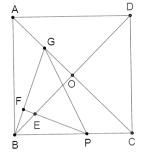
①![]() ;②PE=2BF;③在点P运动的过程中,当GB=GP时,
;②PE=2BF;③在点P运动的过程中,当GB=GP时,![]() ;④当P为BC的中点时,
;④当P为BC的中点时,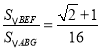 .
.
A.①②③B..①②④C.②③④D..①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
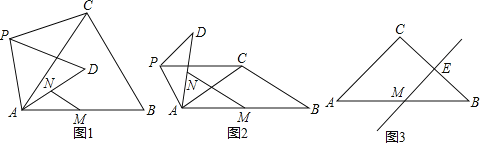
【题目】在![]() 中,
中,![]() ,
,![]() .点P是平面内不与A,C重合的任意一点,连接
.点P是平面内不与A,C重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转
绕点P逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .点M是
.点M是![]() 的中点,点N是
的中点,点N是![]() 的中点.
的中点.
(1)问题发现
如图1,当![]() 时,
时,![]() 的值是________,直线
的值是________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究
如图2,当![]() 时,请写出的
时,请写出的![]() 值及直线
值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
如图3,当![]() 时,若点E是
时,若点E是![]() 的中点,点P在直线
的中点,点P在直线![]() 上,请直接写出点B,P,D在同一条直线上时
上,请直接写出点B,P,D在同一条直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前夕,某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费125元,购进A品牌文具袋3个和B品牌文具袋各4个共花费90元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为y元.
①求y关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不超过进货价格的40%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公路MN为东西走向,在点M北偏东36.5°方向上,距离5千米处是学校A;在点M北偏东45°方向上距离![]() 千米处是学校B.(参考数据:
千米处是学校B.(参考数据:![]() ,
,![]()
![]() ).
).
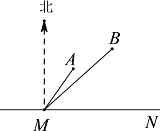
(1)求学校A,B两点之间的距离
(2)要在公路MN旁修建一个体育馆C,使得A,B两所学校到体育馆C的距离之和最短,求这个最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com