
【题目】如图,公路MN为东西走向,在点M北偏东36.5°方向上,距离5千米处是学校A;在点M北偏东45°方向上距离![]() 千米处是学校B.(参考数据:
千米处是学校B.(参考数据:![]() ,
,![]()
![]() ).
).
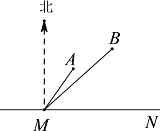
(1)求学校A,B两点之间的距离
(2)要在公路MN旁修建一个体育馆C,使得A,B两所学校到体育馆C的距离之和最短,求这个最短距离.
【答案】(1)![]() km;(2)
km;(2)![]() km.
km.
【解析】
(1)过点A作CD//MN,BE⊥MN,在Rt△ACM中求出CM,AC,在Rt△MBE中求出BE,ME,继而得出AD,BD的长度,在Rt△ABD中利用勾股定理可得出AB的长度.
(2)作点B关于MN的对称点G,连接AG交MN于点P,点P即为站点,求出AG的长度即可.
(1)过点A作CD//MN,BE⊥MN,如图:
在Rt△ACM中,∠CMA=36.5°,AM=5km,
∵sin36.5°=![]() =0.6,
=0.6,
∴CA=3,MC=4km,
在Rt△MBE中,∠NMB=45°,MB=![]() km,
km,
∵sin45°=![]() =
=![]() ,
,
∴BE=6,ME=6km,
∴AD=CDCA=MECA=3km,BD=BEDE=BECM=2km,
在Rt△ABD中,AB=![]() km.
km.
(2)作点B关于MN的对称点G,连接AG交MN于点P,连接PB,点P即为站点,
此时PA+PB=PA+PG=AG,即A,B两所学校到体育馆C的距离之和最短为AG长
在Rt△ADG中,AD=3,DG=DE+EG=DE+BE=4+6=10,∠ADG=90°,
∴AG=![]() =
=![]() km.
km.
答:最短距离为![]() km.
km.



科目:初中数学 来源: 题型:
【题目】AB是![]() 的直径,点C是
的直径,点C是![]() 上一点,连接AC、BC,直线MN过点C,满足
上一点,连接AC、BC,直线MN过点C,满足![]() .
.
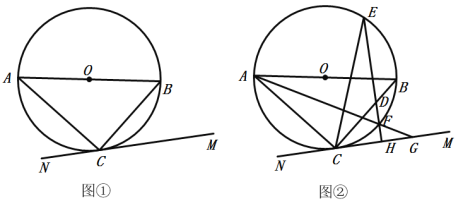
(1)如图①,求证:直线MN是![]() 的切线;
的切线;
(2)如图②,点D在线段BC上,过点D作![]() 于点H,直线DH交
于点H,直线DH交![]() 于点E、F,连接AF并延长交直线MN于点G,连接CE,且
于点E、F,连接AF并延长交直线MN于点G,连接CE,且![]() ,若
,若![]() 的半径为1,
的半径为1,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题与情境)
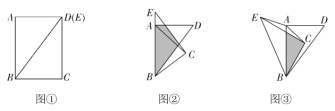
在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图①,现有矩形纸片![]() .连接
.连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 位置不变,将
位置不变,将![]() 从图①的位置开始,绕点B按逆时针方向旋转,旋转角为
从图①的位置开始,绕点B按逆时针方向旋转,旋转角为![]() .
.
(操作发现)
(1)在![]() 旋转过程中,连接
旋转过程中,连接![]() ,则当
,则当![]() 时,
时,![]() 的值是________;
的值是________;
(2)如图②,将图①中的![]() 旋转,当点E落在
旋转,当点E落在![]() 延长线上时停止旋转,求出此时
延长线上时停止旋转,求出此时![]() 的值;
的值;
(实践探究)
(3)如图③,将图②中的![]() 继续旋转,当
继续旋转,当![]() 时停止旋转,直接写出此时
时停止旋转,直接写出此时![]() 的度数,并求出
的度数,并求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
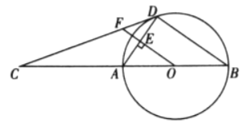
【题目】如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)求证:∠ADC=∠AOF;
(2)若sinC=![]() ,BD=8,求EF的长.
,BD=8,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
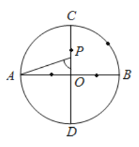
【题目】如图,![]() 是
是![]() 的两条互相垂直的直径,点P从点O出发,沿
的两条互相垂直的直径,点P从点O出发,沿![]() 的路线匀速运动,设
的路线匀速运动,设![]() (单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )
(单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )
A.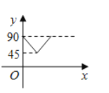 B.
B.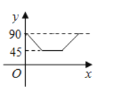 C.
C.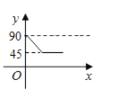 D.
D.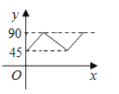
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某校初二年级的同学乘坐大巴车去北京展览馆参观“砥砺奋进的五年”大型成就展,北京展览馆距离该校12千米,1号车出发3分钟后,2号车才出发,结果两车同时到达,已知2号车的平均速度是1号车的平均速度的1.2倍,求2号车的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
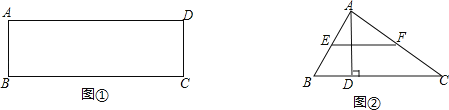
【题目】(1)如图①,在矩形ABCD中,在BC边上是否存在点P,使∠APD=90°,若存在请用直尺和圆规作出点P(保留作图痕迹)
(2)若AB=4,AD=10,求出图①中BP的长.
(3)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为AB,AC的中点,当AD=6时,BC边上是否存在一点Q,使∠EQF=90°,求此时BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
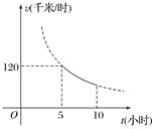
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个盒子中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色.请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com