
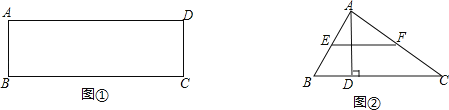
【题目】(1)如图①,在矩形ABCD中,在BC边上是否存在点P,使∠APD=90°,若存在请用直尺和圆规作出点P(保留作图痕迹)
(2)若AB=4,AD=10,求出图①中BP的长.
(3)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为AB,AC的中点,当AD=6时,BC边上是否存在一点Q,使∠EQF=90°,求此时BQ的长.
【答案】(1)作图见解析;(2)BP的长是2或8;(3)![]() .
.
【解析】
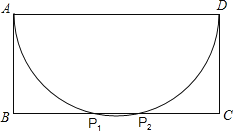
(1)以AD为直径画圆与BC交于点P1、P2,则点P1、P2为所求点;
(2)由矩形的性质得到AD=BC=10,AB=CD=4根据三角形相似即可解出;
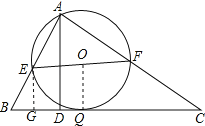
(3)由三角形的中位线得到EF∥BC,EF=![]() BC=6,根据EF与BC间距离为3,推出以EF为直径的⊙O与BC相切,得出BC上符合条件的点Q只有一个,记⊙O与BC相切于点Q,连接OQ,过点E作EG⊥BC,垂足为G,证出四边形EOQG为正方形,由勾股定理即可求出.
BC=6,根据EF与BC间距离为3,推出以EF为直径的⊙O与BC相切,得出BC上符合条件的点Q只有一个,记⊙O与BC相切于点Q,连接OQ,过点E作EG⊥BC,垂足为G,证出四边形EOQG为正方形,由勾股定理即可求出.
解:(1)如图所示,则点P1、P2为所求点;
(2)在矩形ABCD中,AD=BC=10,AB=CD=4,
设BP=x,则PC=10﹣x,
∵∠APD=90°,
∴∠APB+∠CPD=90°,
∵∠BAP+∠APB=90°,
∴∠BAP=∠CPD,
又∵∠B=∠C=90°,
∴△ABP∽△PCD,
∴![]() ,
,
∴![]() ,
,
解得:x1=2,x2=8,
∴BP的长是2或8;
(3)如图:
∵EF分别为AB、AC的中点,
∴EF∥BC,EF=![]() BC=6,
BC=6,
∵AD=6,AD⊥BC,
∴EF与BC间距离为3,
∴以EF为直径的⊙O与BC相切,
∴BC上符合条件的点Q只有一个,记⊙O与BC相切于点Q,
连接OQ,过点E作EG⊥BC,垂足为G,
∴EG=OE=3,
∴四边形EOQG为正方形,
在Rt△EBG中,∠B=60°,EG=3,∴![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .点P是平面内不与A,C重合的任意一点,连接
.点P是平面内不与A,C重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转
绕点P逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .点M是
.点M是![]() 的中点,点N是
的中点,点N是![]() 的中点.
的中点.
(1)问题发现
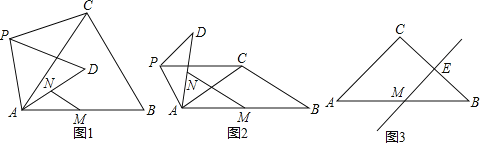
如图1,当![]() 时,
时,![]() 的值是________,直线
的值是________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究
如图2,当![]() 时,请写出的
时,请写出的![]() 值及直线
值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
如图3,当![]() 时,若点E是
时,若点E是![]() 的中点,点P在直线
的中点,点P在直线![]() 上,请直接写出点B,P,D在同一条直线上时
上,请直接写出点B,P,D在同一条直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4.D是边AB的中点,点E为边AC上的一个动点(与点A、C不重合),过点E作EF∥AB,交边BC于点F.联结DE、DF,设CE=x.

(1)当x =1时,求△DEF的面积;
(2)如果点D关于EF的对称点为D’,点D’ 恰好落在边AC上时,求x的值;
(3)以点A为圆心,AE长为半径的圆与以点F为圆心,EF长为半径的圆相交,另一个交点H恰好落在线段DE上,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公路MN为东西走向,在点M北偏东36.5°方向上,距离5千米处是学校A;在点M北偏东45°方向上距离![]() 千米处是学校B.(参考数据:
千米处是学校B.(参考数据:![]() ,
,![]()
![]() ).
).
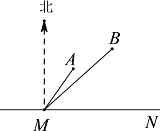
(1)求学校A,B两点之间的距离
(2)要在公路MN旁修建一个体育馆C,使得A,B两所学校到体育馆C的距离之和最短,求这个最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行钢笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图.
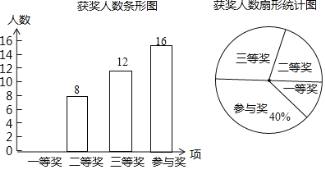
请结合图中相关信息解答下列问题:
(1)扇形统计图中三等奖所在扇形的圆心角的度数是______度;
(2)请将条形统计图补全;
(3)获得一等奖的同学中有![]() 来自七年级,有
来自七年级,有![]() 来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
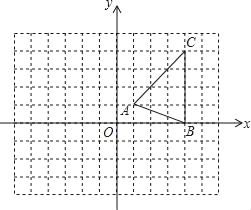
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用![]() (元)随时间
(元)随时间![]() (天)的变化图象为折线
(天)的变化图象为折线![]() ,如图所示.
,如图所示.
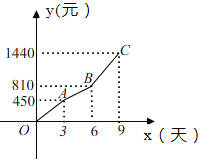
(1)当租赁时间不超过3天时,求每日租金.
(2)当![]() 时,求
时,求![]() (元)与
(元)与![]() (天)的函数关系式.
(天)的函数关系式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁的时间共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015德阳)大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com