
����Ŀ��ij��ѧ���иֱ��鷨�������Ը��꼶ͬѧ�Ļ����������ͳ�ƣ�������������������������ͳ��ͼ��
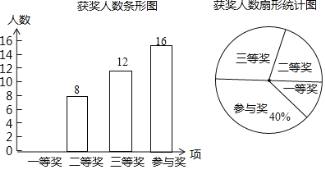
����ͼ�������Ϣ����������⣺
(1)����ͳ��ͼ�����Ƚ��������ε�Բ�ĽǵĶ�����______�ȣ�
(2)�뽫����ͳ��ͼ��ȫ��
(3)���һ�Ƚ���ͬѧ����![]() �������꼶����
�������꼶����![]() ���Ծ��꼶������ͬѧ�������꼶�������ӻ��һ�Ƚ���ͬѧ����ѡ2�˲μ��м��ֱ��鷨��������ͨ���б�����״ͼ�ķ�������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ�ĸ��ʣ�
���Ծ��꼶������ͬѧ�������꼶�������ӻ��һ�Ƚ���ͬѧ����ѡ2�˲μ��м��ֱ��鷨��������ͨ���б�����״ͼ�ķ�������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ�ĸ��ʣ�
���𰸡�(1)108��(2)��ͼ��������(3)![]() .
.
��������
(1)�ȸ��ݲ��뽱������������ռ�ٷֱ����������������![]() �������Ƚ�������ռ�������ɵô𰸣�(2)�������������һ�Ƚ�����������ȫͼ�μ��ɣ�(3)����״ͼ�ó����еȿ��ܽ�����ٴ����ҵ����������Ľ���������ø��ʹ�ʽ���㼴�ɵô𰸣�
�������Ƚ�������ռ�������ɵô𰸣�(2)�������������һ�Ƚ�����������ȫͼ�μ��ɣ�(3)����״ͼ�ó����еȿ��ܽ�����ٴ����ҵ����������Ľ���������ø��ʹ�ʽ���㼴�ɵô𰸣�
(1)�߱������������Ϊ![]() (��)��
(��)��
������ͳ��ͼ�����Ƚ��������ε�Բ�ĽǵĶ�����![]() ��
��
�ʴ�Ϊ��108��
(2)һ�Ƚ�����Ϊ![]() (��)��
(��)��
��ȫͼ�����£�
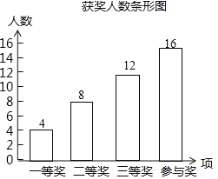
(3)һ�Ƚ��У����꼶����Ϊ![]() (��)�����꼶����Ϊ
(��)�����꼶����Ϊ![]() (��)������꼶����2�ˣ�
(��)������꼶����2�ˣ�
����״ͼ���£�
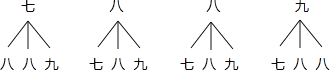
����״ͼ֪������12�ֵȿ��ܽ����������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ����4�ֽ����
������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ�ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
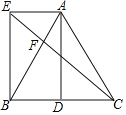
����Ŀ����ͼ������ABC�У�AB��AC��DΪBC�е㣬AE��BD����AE��BD��
��1����֤���ı���AEBD�Ǿ��Σ�
��2������CE��AB�ڵ�F������ABE��30����AE��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������������ͬһ��·��A�س���ǰ��·��Ϊ100ǧ��B�أ��ҳ��ȼ׳�������15���ӣ���ʻ����������ʻ��·�̷ֱ���y1��y2��ǧ�ף���ʾ��������׳���ʻ��ʱ��x�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ.

��1���ֱ����y1��y2����x�ĺ�������ʽ��д��������
��2���ҳ���ʻ�ʱ���ϼ׳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
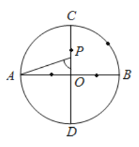
����Ŀ����ͼ��![]() ��
��![]() ���������ഹֱ��ֱ������P�ӵ�O��������
���������ഹֱ��ֱ������P�ӵ�O��������![]() ��·�������˶�����
��·�������˶�����![]() ����λ���ȣ�����ôy���P�˶���ʱ�䣨��λ���룩�Ĺ�ϵͼ�ǣ� ��
����λ���ȣ�����ôy���P�˶���ʱ�䣨��λ���룩�Ĺ�ϵͼ�ǣ� ��
A.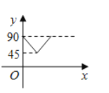 B.
B.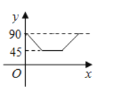 C.
C.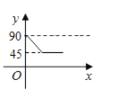 D.
D.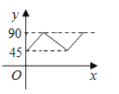
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() ��OAƽ��
��OAƽ��![]() ��BC�ڵ�O����OΪԲ�ģ�OC��Ϊ�뾶��Բ��BC�ڵ�D��
��BC�ڵ�O����OΪԲ�ģ�OC��Ϊ�뾶��Բ��BC�ڵ�D��

��1����ͼ1����֤��ABΪ![]() �����ߣ�
�����ߣ�
��2����ͼ2��AB��![]() �����ڵ�E������CE��OA�ڵ�F��
�����ڵ�E������CE��OA�ڵ�F��
�����ж��߶�OA��CE�Ĺ�ϵ����˵�����ɣ�
����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ�٣��ھ���ABCD�У���BC�����Ƿ���ڵ�P��ʹ��APD��90��������������ֱ�ߺ�Բ��������P��������ͼ�ۼ���
��2����AB��4��AD��10�����ͼ����BP�ij���
��3����ͼ�ڣ�����ABC�У���ABC��60����BC��12��AD��BC���ϵĸߣ�E��F�ֱ�ΪAB��AC���е㣬��AD��6ʱ��BC�����Ƿ����һ��Q��ʹ��EQF��90�������ʱBQ�ij���
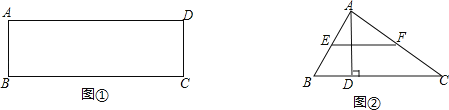
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����k+1��x+![]() k2+1=0������ʵ������
k2+1=0������ʵ������
��1����k��ȡֵ��Χ��
��2�������̵���ʵ�����ֱ�Ϊx1��x2����x12+x22=6x1x2��15����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʳƷ������һ�ְ��Ʒʳ�ģ�����![]() ��ǧ��
��ǧ��![]() �����ۼ۸�
�����ۼ۸�![]() Ԫ
Ԫ![]() ǧ��
ǧ��![]() ���㺯����ϵʽ
���㺯����ϵʽ![]() �����г���������Ϣ���֣��ð��Ʒʳ�ĵ��г�������
�����г���������Ϣ���֣��ð��Ʒʳ�ĵ��г�������![]() ��ǧ��
��ǧ��![]() �����ۼ۸�
�����ۼ۸�![]() Ԫ
Ԫ![]() ǧ��
ǧ��![]() ����һ�κ�����ϵ�����±���
����һ�κ�����ϵ�����±���
���ۼ۸� | 2 | 4 |
| 10 |
������� | 12 | 10 |
| 4 |
��֪����۲��Ź涨���ۼ۸�x������2Ԫ![]() ǧ���Ҳ�����10Ԫ
ǧ���Ҳ�����10Ԫ![]() ǧ��
ǧ��
![]() ��q��x�ĺ�����ϵʽ��
��q��x�ĺ�����ϵʽ��
![]() ������С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳������ʱx��ȡֵ��Χ��
������С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳������ʱx��ȡֵ��Χ��
![]() �����������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ���
�����������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ���![]() ���ð��Ʒʳ�ĵijɱ���2Ԫ
���ð��Ʒʳ�ĵijɱ���2Ԫ![]() ǧ�ˣ�
ǧ�ˣ�
![]() �һ�õ�����
�һ�õ�����![]() ��Ԫ
��Ԫ![]() �����ۼ۸�x�ĺ�����ϵʽ��
�����ۼ۸�x�ĺ�����ϵʽ��
![]() �����һ�õ�����
�����һ�õ�����![]() ��Ԫ
��Ԫ![]() �����ۼ۸�x�����Ƕ�����ʱ��ֱ��д��x��ȡֵ��Χ
�����ۼ۸�x�����Ƕ�����ʱ��ֱ��д��x��ȡֵ��Χ![]() ����
����![]() �ۼ�
�ۼ�![]() �ɱ�
�ɱ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ��������ʵ��ͼ��ͼ2���乤��ʾ��ͼ��AC�ǿ������������رۣ���ת����A�����BD�ĸ߶�AHΪ3.4m�������ر�AC����Ϊ9m���Žǡ�HACΪ118��ʱ�������ƽ̨C�����ĸ߶ȣ��������С�����һλ���ο����ݣ�sin28���0.47��cos28���0.88��tan28���0.53��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com