
【题目】在平面直角坐标系xOy中,A(t,0),B(t+4,0),线段AB的中点为C,若平面内存在一点P使得∠APC或者∠BPC为直角(点P不与A,B,C重合),则称P为线段AB的直角点.
(1)当t=0时,
①在点P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,线段AB的直角点是 ;
)中,线段AB的直角点是 ;
②直线y=![]() x+b上存在四个线段AB的直角点,直接写出b取值范围;
x+b上存在四个线段AB的直角点,直接写出b取值范围;
(2)直线y=![]() x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
【答案】(1)①![]() ,
,![]() ②
②![]() 或
或![]() (2)
(2)![]() 或
或![]()
【解析】
(1)由线段AB的直角点定义可求解;
(2)由圆周角定理可得点P在以BC为直径或AC为直径的圆上,求出直线y=![]() x+b过点C时,b的值和直线y=
x+b过点C时,b的值和直线y=![]() x+b与以BC为直径或AC为直径的圆相切时,b的值,即可求解.
x+b与以BC为直径或AC为直径的圆相切时,b的值,即可求解.
(3)由题意可得以BC为直径或AC为直径的圆与线段MN的交点只有两个,利用特殊位置可求解.
解:(1)①当t=0时,则点A(0,0),点B(4,0),
∵点C是AB中点,
∴点C(2,0),
∴AC=BC=2,
∵AP12+CP12=![]() +
+![]() ≠AC2=4,
≠AC2=4,
∴点P1不是线段AB的直角点;
∵AP22+CP22=![]() +
+![]() +
+![]() +
+![]() =4=AC2=4,
=4=AC2=4,
∴∠AP2B=90°,
∴点P2是线段AB的直角点,
∵CP32+BP32=![]() +
+![]() +
+![]() +
+![]() =4=BC2=4,
=4=BC2=4,
∴∠CP3B=90°,
∴点P3是线段AB的直角点,
故答案为:P2,P3;
②∵∠APC或者∠BPC为直角,
p>∴点P在以BC为直径或AC为直径的圆上,如图,当直线y=![]() x+b与以AC为直径的圆相切时,直线y=
x+b与以AC为直径的圆相切时,直线y=![]() x+b与以AC为直径的圆和以BC为直径的圆有三个交点,即存在三个线段AB的直角点,
x+b与以AC为直径的圆和以BC为直径的圆有三个交点,即存在三个线段AB的直角点,
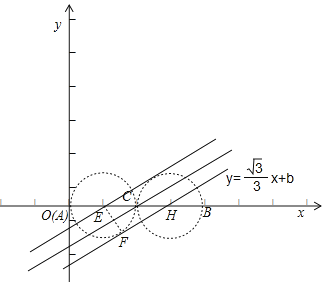
设切点为F,以AC为直径的圆的圆心为E,直线y=![]() x+b与x轴交于点H,连接EF,
x+b与x轴交于点H,连接EF,
∵直线y=![]() x+b与以AC为直径的圆相切,
x+b与以AC为直径的圆相切,
∴EF⊥FH,
∵直线y=![]() x+b与x轴所成锐角为30°,
x+b与x轴所成锐角为30°,
∴EH=2EF=2,
∴点H(3,0),
∴0=![]() ×3+b,
×3+b,
∴b=﹣![]() ,
,
同理可得,当直线y=![]() x+b与以BC为直径的圆相切时,b=﹣
x+b与以BC为直径的圆相切时,b=﹣![]() ,
,
当直线y=![]() x+b过点C时,直线y=
x+b过点C时,直线y=![]() x+b与以AC为直径的圆和以BC为直径的圆有三个交点,即直线y=
x+b与以AC为直径的圆和以BC为直径的圆有三个交点,即直线y=![]() x+b上存在三个线段AB的直角点,
x+b上存在三个线段AB的直角点,
∴0=![]() +b,
+b,
∴b=﹣![]() ,
,
∴当﹣![]() <b<﹣
<b<﹣![]() 或﹣
或﹣![]() <b<﹣
<b<﹣![]() 时,直线y=
时,直线y=![]() x+b与以AC为直径的圆和以BC为直径的圆有四个交点,即直线y=
x+b与以AC为直径的圆和以BC为直径的圆有四个交点,即直线y=![]() x+b上存在四个线段AB的直角点,
x+b上存在四个线段AB的直角点,
(2)∵直线y=![]() x+1与x,y轴交于点M,N,
x+1与x,y轴交于点M,N,
∴点N(0,1),点M(﹣![]() ,0),
,0),
如图,当直线y=![]() x+1与以BC为直径的圆相切于点F,设BC为直径的圆的圆心为E,连接EF,此时线段MN与以AC为直径的圆和以BC为直径的圆有两个交点,即线段MN上存在两个线段AB的直角点,
x+1与以BC为直径的圆相切于点F,设BC为直径的圆的圆心为E,连接EF,此时线段MN与以AC为直径的圆和以BC为直径的圆有两个交点,即线段MN上存在两个线段AB的直角点,
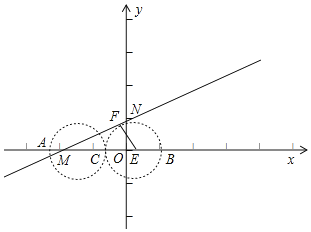
∵A(t,0),B(t+4,0),点C是线段AB的中点,
∴AB=4,AC=BC=2,
∵直线y=![]() x+1与以BC为直径的圆相切于点F,
x+1与以BC为直径的圆相切于点F,
∴EF⊥MN,
∵∠NMB=30°,
∴ME=2EF=2,
∴点E(﹣![]() +2,0),
+2,0),
∴点A(﹣![]() ﹣1,0),
﹣1,0),
∴t=﹣![]() ﹣1
﹣1
当直线y=![]() x+1与以AC为直径的圆相切时,此时线段MN与以AC为直径的圆和以BC为直径的圆有3个交点,即线段MN上存在3个线段AB的直角点,
x+1与以AC为直径的圆相切时,此时线段MN与以AC为直径的圆和以BC为直径的圆有3个交点,即线段MN上存在3个线段AB的直角点,
同理可求:t=1﹣![]() ,
,
当点A与点M重合时,此时线段MN与以AC为直径的圆和以BC为直径的圆有两个交点,即线段MN上存在两个线段AB的直角点,
∴当﹣![]() <t<1﹣
<t<1﹣![]() 或t=﹣
或t=﹣![]() ﹣1时,线段MN上只存在两个线段AB的直角点.
﹣1时,线段MN上只存在两个线段AB的直角点.
【点晴】
本题考查了一次函数的综合应用,角的计算,圆周角定理以及切线的性质;解题的关键是懂得点P在以BC为直径或AC为直径的圆上,以此来解决此题,此题综合性较强,与切线的性质练习较大,在日常练习中应加强训练.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
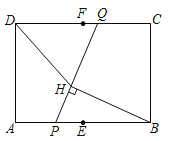
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点.动点
边的中点.动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,同时,动点
运动,同时,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,连接
运动,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 的速度是点
的速度是点![]() 的速度的2倍,在点
的速度的2倍,在点![]() 从点
从点![]() 运动至点
运动至点![]() 的过程中,线段
的过程中,线段![]() 长度的最大值为_________,线段
长度的最大值为_________,线段![]() 长度的最小值为_________.
长度的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)若cos∠PAB=![]() ,BC=2,求PO的长.
,BC=2,求PO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
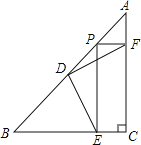
(1)探究DE与DF的关系,并给出证明;
(2)当点P满足什么条件时,线段EF的长最短?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF=![]() ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
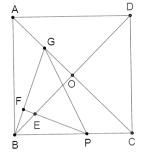
①![]() ;②PE=2BF;③在点P运动的过程中,当GB=GP时,
;②PE=2BF;③在点P运动的过程中,当GB=GP时,![]() ;④当P为BC的中点时,
;④当P为BC的中点时,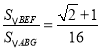 .
.
A.①②③B..①②④C.②③④D..①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com