
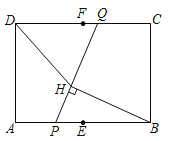
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点.动点
边的中点.动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,同时,动点
运动,同时,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,连接
运动,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 的速度是点
的速度是点![]() 的速度的2倍,在点
的速度的2倍,在点![]() 从点
从点![]() 运动至点
运动至点![]() 的过程中,线段
的过程中,线段![]() 长度的最大值为_________,线段
长度的最大值为_________,线段![]() 长度的最小值为_________.
长度的最小值为_________.
【答案】![]()
![]()
【解析】
连接EF,则EF⊥AB,过点P作PG⊥CD于点G,如图1,由于![]() ,而PG=3,所以当GQ最大时PQ最大,由题意可得当P、A重合时GQ最大,据此即可求出PQ的最大值;设EF与PQ交于点M,连接BM,取BM的中点O,连接HO,如图2,易证△FQM∽△EPM,则根据相似三角形的性质可得EM为定值2,于是BM的长度可得,由∠BHM=∠BEM=90°可得B、E、H、M四点共圆,且圆心为点O,于是当D、H、O三点共线时,DH的长度最小,最小值为DO-OH,为此只需连接DO,求出DO的长即可,可过点O作ON⊥CD于点N,作OK⊥BC于点K,如图3,构建Rt△DON,利用勾股定理即可求出DO的长,进而可得答案.
,而PG=3,所以当GQ最大时PQ最大,由题意可得当P、A重合时GQ最大,据此即可求出PQ的最大值;设EF与PQ交于点M,连接BM,取BM的中点O,连接HO,如图2,易证△FQM∽△EPM,则根据相似三角形的性质可得EM为定值2,于是BM的长度可得,由∠BHM=∠BEM=90°可得B、E、H、M四点共圆,且圆心为点O,于是当D、H、O三点共线时,DH的长度最小,最小值为DO-OH,为此只需连接DO,求出DO的长即可,可过点O作ON⊥CD于点N,作OK⊥BC于点K,如图3,构建Rt△DON,利用勾股定理即可求出DO的长,进而可得答案.
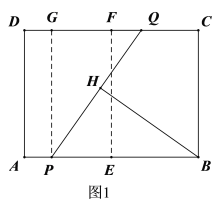
解:连接EF,则EF⊥AB,过点P作PG⊥CD于点G,如图1,则PE=GF,PG=AD=3,
设FQ=t,则GF=PE=2t,GQ=3t,
在Rt△PGQ中,由勾股定理得:![]() ,
,
∴当t最大即EP最大时,PQ最大,
由题意知:当点P、A重合时,EP最大,此时EP=2,则t=1,
∴PQ的最大值=![]() ;
;
设EF与PQ交于点M,连接BM,取BM的中点O,连接HO,如图2,
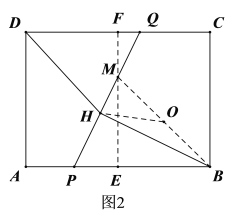
∵FQ∥PE,∴△FQM∽△EPM,
∴![]() ,
,
∵EF=3,
∴FM=1,ME=2,
∴![]() ,
,
∵∠BHM=∠BEM=90°,
∴B、E、H、M四点共圆,且圆心为点O,
∴![]() ,
,
∴当D、H、O三点共线时,DH的长度最小,
连接DO,过点O作ON⊥CD于点N,作OK⊥BC于点K,如图3,则OK=BK=1,
∴NO=2,CN=1,∴DN=3,
则在Rt△DON中,![]() ,
,
∴DH的最小值=DO-OH=![]() .
.
故答案为:![]() ,
,![]() .
.



科目:初中数学 来源: 题型:
【题目】甲、乙两地之间有一条笔直的公路,小明从甲地出发步行前往乙地,同时小亮从乙地出发骑自行车前往甲地,小亮到达甲地没有停留,按原路原速返回,追上小明后两人一起步行到乙地.如图,线段OA表示小明与甲地的距离y1(米)与行走的时间x(分钟)之间的函数关系:折线BCDA表示小亮与甲地的距离y2(米)与行走的时间x(分钟)之间的函数关系.请根据图象解答下列问题:
(1)小明步行的速度是 米/分钟,小亮骑自行车的速度是 米/分钟;
(2)线段OA与BC相交于点E,求点E坐标;
(3)请直接写出小亮从乙地出发到追上小明的过程中,与小明相距100米时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点D是边
,点D是边![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过点D,交
的图象经过点D,交![]() 边于点E,直线
边于点E,直线![]() 的解析式为
的解析式为![]() .
.

(1)求反比例函数![]() 的解析式和直线
的解析式和直线![]() 的解析式;
的解析式;
(2)在y轴上找一点P,使![]() 的周长最小,求出此时点P的坐标;
的周长最小,求出此时点P的坐标;
(3)在(2)的条件下,![]() 的周长最小值是______.
的周长最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
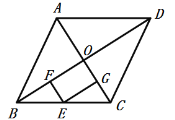
【题目】如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
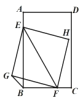
【题目】已知:矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() 同时从点
同时从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 匀速运动,速度均为
匀速运动,速度均为![]() ,当一个点到达终点时另一个点也停止运动.连接
,当一个点到达终点时另一个点也停止运动.连接![]() ,以
,以![]() 为对角线作正方形
为对角线作正方形![]() ,连接
,连接![]() ,则
,则![]() 的长度为____.
的长度为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
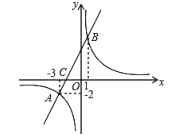
【题目】如图,一次函数![]() 图象与反比例函数
图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式.
的解析式.
(2)求点![]() 坐标.
坐标.
(3)平面上的点![]() 与点
与点![]() 、
、![]() 、
、![]() 构成平行四边形,请直接写出满足条件的
构成平行四边形,请直接写出满足条件的![]() 点坐标______.
点坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位食堂为全体名职工提供了![]() 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取
四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取![]() 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
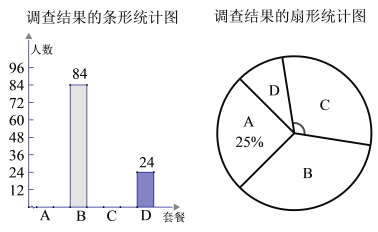
![]() 在抽取的
在抽取的![]() 人中最喜欢
人中最喜欢![]() 套餐的人数为 ,扇形统计图中“
套餐的人数为 ,扇形统计图中“![]() ”对应扇形的圆心角的大小为 ;
”对应扇形的圆心角的大小为 ;
![]() 依据本次调查的结果,估计全体
依据本次调查的结果,估计全体![]() 名职工中最喜欢
名职工中最喜欢![]() 套餐的人数;
套餐的人数;
![]() 现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B(t+4,0),线段AB的中点为C,若平面内存在一点P使得∠APC或者∠BPC为直角(点P不与A,B,C重合),则称P为线段AB的直角点.
(1)当t=0时,
①在点P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,线段AB的直角点是 ;
)中,线段AB的直角点是 ;
②直线y=![]() x+b上存在四个线段AB的直角点,直接写出b取值范围;
x+b上存在四个线段AB的直角点,直接写出b取值范围;
(2)直线y=![]() x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com