
【题目】已知:矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() 同时从点
同时从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 匀速运动,速度均为
匀速运动,速度均为![]() ,当一个点到达终点时另一个点也停止运动.连接
,当一个点到达终点时另一个点也停止运动.连接![]() ,以
,以![]() 为对角线作正方形
为对角线作正方形![]() ,连接
,连接![]() ,则
,则![]() 的长度为____.
的长度为____.
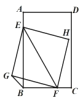
【答案】![]()
【解析】
过点G作GN⊥BC交CB的延长线于N,过点E作EM⊥GN,交NG的延长线于M,通过证明点G,点B,点F,点E四点共圆,可得∠GBE=∠GFE=45°,可得GN=BN,通过证明△MEG≌△NGF,可得MG=NF=BF+BN=6-FC+BN,GN=ME,由线段的和差关系可求BN的长,即可求解.
如图,过点G作GN⊥BC交CB的延长线于N,过点E作EM⊥GN,交NG的延长线于M,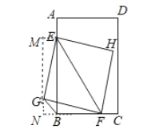
∵点E,点F,速度均为1cm/s,
∴AE=CF,
∵四边形EGFH是正方形,
∴EG=GF,∠EGF=∠ABC=90°,∠EFG=45°,
∴点G,点B,点F,点E四点共圆,
∴∠GBE=∠GFE=45°,
∴∠GBN=45°,
∵GN⊥BC,
∴∠NGB=∠GBN=45°,
∴GN=BN,
∵EM⊥GN,GN⊥BC,∠EBN=90°,
∴四边形EBNM是矩形,
∴BE=MN=8-AE,ME=NB,
∵EM⊥GN,GN⊥BC,
∴∠M=∠N=90°,
∴∠MGE+∠MEG=90°,
又∵∠MGE+∠NGF=90°,
∴∠MEG=∠NGC,
∴△MEG≌△NGF(AAS),
∴MG=NF=BF+BN=6-FC+BN,
GN=ME,
∴MN=MG+GN=6-FC+BN+ME=6-AE+2BN=8-AE,
∴BN=1,
∴GN=BN=1,
∴GB=![]() BN=
BN=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
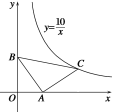
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点A在x轴上,点B的坐标是(0,3),若点C恰好在反比例函数![]() 第一象限内的图象上,那么点C的坐标为______________.
第一象限内的图象上,那么点C的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
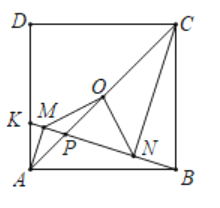
【题目】如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1)求证:AM=BN;
(2)请判断△OMN的形状,并说明理由;
(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为![]() ,请直接写出AK长.
,请直接写出AK长.
查看答案和解析>>
科目:初中数学 来源: 题型:
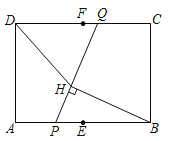
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点.动点
边的中点.动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,同时,动点
运动,同时,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,连接
运动,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 的速度是点
的速度是点![]() 的速度的2倍,在点
的速度的2倍,在点![]() 从点
从点![]() 运动至点
运动至点![]() 的过程中,线段
的过程中,线段![]() 长度的最大值为_________,线段
长度的最大值为_________,线段![]() 长度的最小值为_________.
长度的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,按学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:
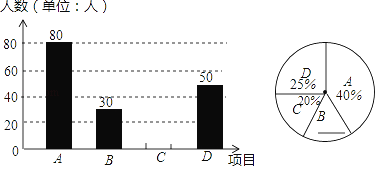
(1)本次共调查了________名学生;
(2)在扇形统计图中,“B”所在扇形的圆心角是________度;
(3)将条形统计图补充完整;
(4)若该中学有1200名学生,喜欢篮球运动的学生约有________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
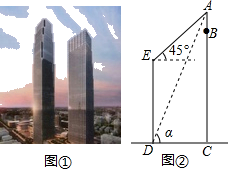
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的综合素养,某校开设了五门手工活动课.按照类别分为:![]() “剪纸”、
“剪纸”、![]() “沙画”、
“沙画”、![]() “葫芦雕刻”、
“葫芦雕刻”、![]() “泥塑”、
“泥塑”、![]() “插花”.为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如下两幅不完整的统计图.
“插花”.为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如下两幅不完整的统计图.
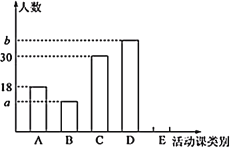
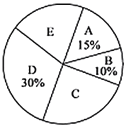
根据以上信息,回答下列问题:
(1)本次调查的样本容量为________;统计图中的![]() ________,
________,![]() ________;
________;
(2)通过计算补全条形统计图;
(3)该校共有2500名学生,请你估计全校喜爱“葫芦雕刻”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
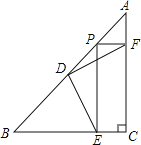
(1)探究DE与DF的关系,并给出证明;
(2)当点P满足什么条件时,线段EF的长最短?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com