
【题目】如图,一次函数![]() 图象与反比例函数
图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
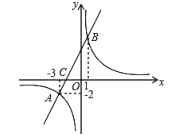
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式.
的解析式.
(2)求点![]() 坐标.
坐标.
(3)平面上的点![]() 与点
与点![]() 、
、![]() 、
、![]() 构成平行四边形,请直接写出满足条件的
构成平行四边形,请直接写出满足条件的![]() 点坐标______.
点坐标______.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)先由图形得出的信息代入求出m,再求出B点,利用待定系数法将A、B代入求出即可.
(2)一次函数令y=0求出x即可得出C坐标.
(3)根据题意分别找到点所在的直线,再根据线段长度判断即可.
解:(1)把![]() 代入
代入![]() 得:
得:![]() ,
,
把![]() 横坐标
横坐标![]() 代入
代入![]() 得:
得:![]() ,即
,即![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴一次函数解析式为![]() ;反比例函数的解析式
;反比例函数的解析式![]() .
.
(2)对于![]() ,
,
令![]() ,得到
,得到![]() ,
,
则![]() 的坐标为
的坐标为![]() ;
;
(3)如下图所示,分三种情况考虑:
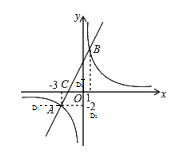
O、C、A三点确定,D点满足题意得点必定在y轴上或过点A平行x轴的平行线上,
在y轴上可得(1,2)、(﹣1,﹣2)满足
在过A点平行x轴的平行线上可得(﹣5,﹣2),(﹣1,﹣2)满足
综上所述:![]() ;
;![]() ;
;![]() .
.
故答案为:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
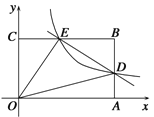
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(6,4).双曲线![]() 经过AB的中点D,且与BC交于点E,连接DE.
经过AB的中点D,且与BC交于点E,连接DE.
(1)求k的值和直线DE的解析式;
(2)若点P是y轴上一点,且△OPE的面积与四边形ODBE的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织了一次全校![]() 名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于
名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于![]() 分,为了更好的了解本次大赛的成绩分布情况,随机抽取了
分,为了更好的了解本次大赛的成绩分布情况,随机抽取了![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行整理,得到下列不完整的统计图表:
分)作为样本进行整理,得到下列不完整的统计图表:
成绩在这![]() 组的数据是:
组的数据是:
![]()
![]()
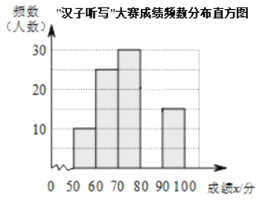
“汉字听写”大赛成绩段频数频率统计表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)表中![]() ,
,![]() ;
;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生获得优胜奖,估计该校参加这次比赛的
分)的学生获得优胜奖,估计该校参加这次比赛的![]() 名学生中获得优胜奖的人数.
名学生中获得优胜奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
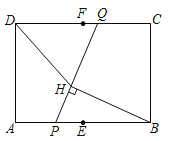
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点.动点
边的中点.动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,同时,动点
运动,同时,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,连接
运动,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 的速度是点
的速度是点![]() 的速度的2倍,在点
的速度的2倍,在点![]() 从点
从点![]() 运动至点
运动至点![]() 的过程中,线段
的过程中,线段![]() 长度的最大值为_________,线段
长度的最大值为_________,线段![]() 长度的最小值为_________.
长度的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在防疫工作稳步推进的过程中,复工复产工作也在如火如荼进行.某企业计划通过扩大生产能力来消化第一季度积累的订单,决定增加一条新的生产线并招收工人.根据以往经验,一名熟练工人每小时完成的工件数量比一名普通工人每小时完成的工件数量多10个,且一名熟练工人完成160个工件与一名普通工人完成80个工件所用的时间相同.
(1)求一名熟练工人和一名普通工人每小时分别能完成多少个工件;
(2)新生产线的目标产能是每小时生产200个工件,计划招聘![]() 名普通工人与
名普通工人与![]() 名熟练工人共同完成这项任务,请写出
名熟练工人共同完成这项任务,请写出![]() 与
与![]() 的函数关系式(不需要写自变量
的函数关系式(不需要写自变量![]() 的取值范围);
的取值范围);
(3)该企业在做市场调研时发现,一名普通工人每天工资为120元,一名熟练工人每天工资为150元,而且本地区现有熟练工人不超过8人.在(2)的条件下,该企业如何招聘工人,使得工人工资的总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
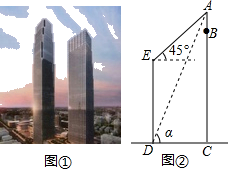
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交边
的角平分线交边![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上以每秒
上以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向从点
方向从点![]() 开始运动,过点
开始运动,过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边向右作平行四边形
为边向右作平行四边形![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() ,设
,设![]() 点运动时间为
点运动时间为![]() 秒.
秒.
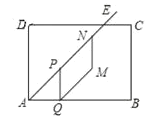
(1)![]() ____________(用含
____________(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与矩形
与矩形![]() 重合部分面积为
重合部分面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)直接写出在点![]() 、
、![]() 运动的过程中,整个图形中形成的三角形存在全等三角形时
运动的过程中,整个图形中形成的三角形存在全等三角形时![]() 的值(不添加任何辅助线).
的值(不添加任何辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com