
【题目】已知![]() 的半径为
的半径为![]() ,
,![]() 的半径为
的半径为![]() ,以
,以![]() 为圆心,以
为圆心,以![]() 的长为半径画弧,再以线段
的长为半径画弧,再以线段![]() 的中点P为圆心,以
的中点P为圆心,以![]() 的长为半径画弧,两弧交于点A,连接
的长为半径画弧,两弧交于点A,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点B,过点B作
于点B,过点B作![]() 的平行线
的平行线![]() 交
交![]() 于点C.
于点C.
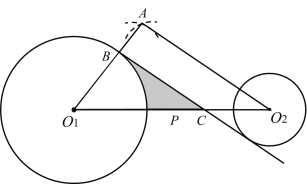
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)过点O2作O2D⊥BC,交BC于点D,根据作图过程可得AP=O1P=O2P,利用等腰三角形的性质和三角形内角和证明AO2⊥AO1,再根据BC∥AO2,证明四边形ABDO2为矩形,得到O2D=![]() ,点D在圆O2上,可得结论;
,点D在圆O2上,可得结论;
(2)证明△AO1O2∽△BO1C,求出O1C,利用△BO1C的面积减去扇形BO1E的面积即可.
解:(1)由作图过程可得:
AP=O1P=O2P=![]() O1O2,AO1=AB+BO1=
O1O2,AO1=AB+BO1=![]() ,
,
∴∠PAO1=PO1A,∠PAO2=∠PO2A,AB=![]() ,
,
而∠PAO1+∠PO1A+∠PAO2+∠PO2A=180°,
∴∠PAO1+∠PAO2=90°,即AO2⊥AO1,
∵BC∥AO2,
∴O1B⊥BC,即BC与圆O1相切,
过点O2作O2D⊥BC,交BC于点D,
可知四边形ABDO2为矩形,
∴AB=O2D=![]() ,而圆O2的半径为
,而圆O2的半径为![]() ,
,
∴点D在圆O2上,
即BC是![]() 的切线;
的切线;
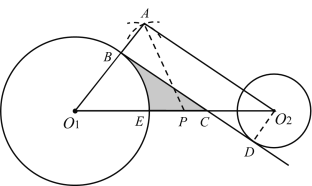
(2)∵AO2∥BC,
∴△AO1O2∽△BO1C,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
即AO1=![]() =3,BO1=2,
=3,BO1=2,
∴![]() ,
,
∴O1C=4,
∵BO1⊥BC,
∴cos∠BO1C=![]() ,
,
∴∠BO1C=60°,
∴BC=![]() ,
,
∴S阴影=![]() -
-![]()
=![]()
=![]()


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
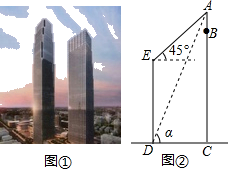
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
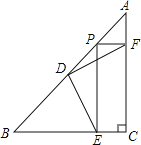
(1)探究DE与DF的关系,并给出证明;
(2)当点P满足什么条件时,线段EF的长最短?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线![]() ,点A、B分别在
,点A、B分别在![]() 、
、![]() 上,斜坡AB的长为18米,过点B作
上,斜坡AB的长为18米,过点B作![]() 于点C,且线段AC的长为
于点C,且线段AC的长为![]() 米.
米.
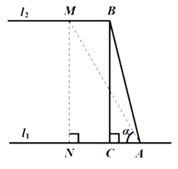
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚![]() 为60°,过点M作
为60°,过点M作![]() 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF=![]() ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
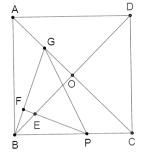
①![]() ;②PE=2BF;③在点P运动的过程中,当GB=GP时,
;②PE=2BF;③在点P运动的过程中,当GB=GP时,![]() ;④当P为BC的中点时,
;④当P为BC的中点时,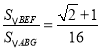 .
.
A.①②③B..①②④C.②③④D..①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大润发”、“世纪联华”两家超市出售同样的洗衣液和香皂,洗衣液和香皂在两家超市的售价分别一样.已知买1袋洗衣液和2块香皂要花费48元,买3袋洗衣液和4块香皂要花费134元.
(1)一袋洗衣液与一块香皂售价各是多少元?(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“大润发”超市规定:这两种商品都打八五折;“世纪联华”超市规定:买一袋洗衣液赠送一块香皂.若妈妈想要买4袋洗衣液和10块香皂,又只能在一家超市购买,你觉得选择哪家超市购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦
中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦![]() (
(![]() 分别为点A,B的对应点),线段
分别为点A,B的对应点),线段![]() 长度的最小值称为线段AB到⊙O的“平移距离”.
长度的最小值称为线段AB到⊙O的“平移距离”.
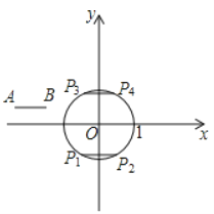
(1)如图,平移线段AB到⊙O的长度为1的弦![]() 和
和![]() ,则这两条弦的位置关系是 ;在点
,则这两条弦的位置关系是 ;在点![]() 中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线![]() 上,记线段AB到⊙O的“平移距离”为
上,记线段AB到⊙O的“平移距离”为![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点A的坐标为![]() ,记线段AB到⊙O的“平移距离”为
,记线段AB到⊙O的“平移距离”为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com